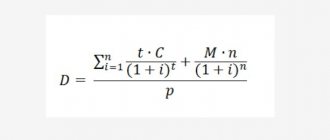Дюрация облигации – это срок, по истечении которого инвестор сможет полностью окупить свои первоначальные вложения. Рассчитывается по достаточно сложной формуле, запоминать которую не обязательно. Важно лишь понимать, что дюрация исчисляется в годах либо в днях и определяется путем вычисления средневзвешенной величины.
Главный показатель, который характеризует дюрация, – это процентный риск. Инвестору, в портфеле которого есть долговые обязательства, необходимо иметь общее представление о том, как вычисляется дюрация облигации. Для расчета можно использовать различные онлайн-сервисы.
В этой статье мы разберем, что такое дюрация облигации простыми словами, приведем формулы и рассчитаем этот показатель на примерах.
Для чего нужна и где применяется
Итак, дюрация облигации – это срок окупаемости вложений в ценную бумагу. Для облигации с нулевым купоном эта величина равна сроку жизни долгового обязательства. Мы будем рассматривать подробно дюрацию купонной облигации и для начала приведем основные определения, которые нам понадобятся.
Облигация – это долговое обязательство государства или компании, по которому эмитент (заемщик) обязуется вернуть приобретателю (кредитору) номинальную стоимость ценной бумаги плюс процент (купон) в течение определенного срока.
Купон – это вознаграждение по облигации, выраженное в процентах к ее номиналу.
Накопленный купонный доход (НКД) – это сумма всех выплат по купону. Такие выплаты могут производиться с различной периодичностью:
- ежегодно;
- раз в полгода;
- ежеквартально.
Чем чаще производятся выплаты, тем сложнее расчет дюрации.
Ставка дисконтирования – это процент ожидаемой прибыли на будущее.
Кроме облигаций, дюрация применяется также для расчета срока окупаемости портфелей, кредитов и других долговых обязательств, инвестиционных проектов. С помощью этого показателя можно рассчитать срок погашения задолженности кредитором.
Суть простыми словами
Дюрация – это когда выплаты по купонам окупают стоимость покупки облигации. Срок окупаемости учитывает все купонные платежи, выплаченные в разное время, и различные особенности облигации, такие как амортизация или оферта. Если купонных платежей, амортизации и оферты нет, то дюрация совпадает со сроком до погашения облигации.
Суть. Очень упрощенно, но смысл примерно такой. Когда вы покупаете облигацию, вы платите её рыночную стоимость. Рыночная стоимость указывается в процентах от номинальной стоимости. Пусть наша облигация будет стоить 101%. При номинальной стоимости 1000 рублей, мы купим её за 1010 рублей. Она приносит нам 50 рублей в год. Допустим срок погашения у неё через 50 лет. Значит окупится она за счет купонов раньше: 1010/50 = 20.2. Т.е. примерно через 20 лет – это и есть дюрация.
Чем больше времени до погашения, тем больше дюрация: инвестор будет дольше возвращать свои деньги. И наоборот: если купонные платежи большие и более частые, а времени до погашения немного, то дюрация будет меньше, потому что инвестор быстрее вернет свои деньги.
Если представить, что предполагаемые платежи — это денежные мешки, расставленные на детских качелях, то:
- расстояния между ними — это промежутки между платежами;
- величина мешков — объем выплаченных средств (один самый большой — это последний поток наличности);
- количество купюр в них — стоимость каждой из выплат.
Чтобы уравновесить качели, на которых стоит некое количество мешочков и один большой «баул» с деньгами, мы должны выбрать точку равновесия. Показателем дюрации в этой модели будет расстояние от найденной точки до начала качелей.
Эффективная дюрация и оферта
Более точной является формула эффективной дюрации облигаций, где учитываются изменения процентной ставки как в большую, так и в меньшую сторону. Эта формула подходит для облигаций с офертой, по которым предусмотрена возможность выкупа до срока погашения.
\[ D_e=\frac{P_{i-} – P_{i+}}{P_0*(i_+ – i_-)} , где \]
\( P_{i-} \) - рыночная цена в случае понижения ставок;
\( P_{i+} \)- рыночная цена в случае повышения ставок;
\( P_0 \)– исходная цена;
\( i_+ \)- размер повышенной ставки;
\( i_- \)- размер пониженной ставки.
Предположим, что ставка может измениться на 2 % в большую и на 3 % в меньшую сторону. Тогда, используя предыдущие расчеты, получим:
\( P_{i+} \)=25-(25*1,39*2/100)=1 826 руб. (24,34 $ или 706 грн.);
\( P_{i-} \)=25+(25*1,39*3/100)=1 953 руб. (26,04 $ или 755 грн.);
\( i_+ \)= 12 %;
\( i_- \)= 7 %.
\[ D_e=\frac{26,04-24,34}{25*(12-7)}=0,01 \]
Значение, близкое к нулю, говорит о низкой чувствительности рыночной стоимости долгового обязательства к изменению процентных ставок. Простыми словами, низкая дюрация – это показатель низкого уровня риска.
Соответственно, облигация с большей дюрацией представляет более высокий риск и более длительный срок окупаемости.
Этой формулой следует пользоваться, если правительство готовит постановления об изменении ставки Центробанка.
Резюме
Дюрация происходит от анг. duration (в переводе «длительность») и означает период, необходимый, чтобы вернуть вложенные в облигацию средства, с учетом размера и периодичности купонных выплат. Дюрация — временная характеристика, поэтому измеряется в днях/годах и меняется ежедневно.
Дюрация используется при сравнении облигаций. Более надежными считаются облигации с меньшей дюрацией.
Чем ниже дюрация, тем меньше влияние изменения процентных ставок. Чтобы понять, как изменится цена облигации при изменении процентных ставок, пользуйтесь значением стоимости базисного пункта.
Если ожидается рост процентных ставок, то предпочтительнее облигации с меньшей дюрацией, если снижение — с большей.
Надеюсь, что после прочтения данной статьи вы разберетесь с таким параметром облигаций, как дюрация, с которым у многих начинающих инвесторов возникают сложности в понимании, и у вас не возникнет трудностей при выборе подходящих облигаций для покупки.
Дюрация портфеля облигаций
Дюрация портфеля рассчитывается путем определения средневзвешенной величины сроков окупаемости ценных бумаг, входящих в портфель. При этом учитывается их процентное соотношение.
Пример. Портфель инвестора состоит из пяти видов ОФЗ.
| Облигация | D, лет | Доля в портфеле, % |
| 1 | 2,68 | 20 |
| 2 | 1,92 | 20 |
| 3 | 1,89 | 20 |
| 4 | 2,14 | 20 |
| 5 | 2,87 | 20 |
\[ Dport=2,68*0,2+1,92*0,2+1,89*0,2+2,14*0,2+2,87*0,2=2,3 г. \]
Таким образом, дюрация портфеля – это средний срок, в течение которого инвестор возместит первоначальные вложения.
Здесь нужно учитывать то, что если ребалансировка производилась до срока погашения, то дюрация портфеля облигаций должна рассчитываться заново. При этом показатель по проданным ценным бумагам должен приниматься как фактический срок нахождения в портфеле. Простыми словами, если облигация со сроком погашения 3 года была продана через 2, то ее дюрация составит 2 года. Размер денежного потока следует исчислять с учетом НКД.
Модифицированная дюрация
Модифицированная дюрация — это второй способ измерения дюрации. С ее помощью инвестор определяет, на сколько процентов изменится цена облигации, если изменятся процентные ставки.
MD = Дюрация Маколея / (1 + процентная ставка)
Для небольших изменений работает следующая формула:
Изменение цены / Рыночная цена с НКД = −MD × Изменение ставок
Учитывая, что в QUIK дюрация Маколея измеряется в днях, полученное значение необходимо разделить еще на 365.
Модифицированная дюрация является безразмерной величиной, а ее математический смысл заключается в следующем: модифицированная дюрация является приближенным изменением стоимости облигации в ответ на изменение доходности на 1% (100 базисных пунктов).
Например, MD равна 3, цена облигации с учетом НКД — 95%, доходность к погашению — 8% годовых. Мы можем определить, как изменится цена, если доходность вырастет на 0,5 процентного пункта и станет равна 8,5%.
Х / 0,95 = −3 × 0,005
Х = −3 × 0,005 × 0,95 = −0,01425
Если доходность вырастет на 0,5%, цена облигации снизится на 1,4%.
Дюрация проекта
Срок окупаемости определяется не только для инвестиций в ценные бумаги, но и для различных бизнес-проектов.
Пример. Компания запускает новый бизнес проект с начальным размером инвестиций – 22 500 000 руб. (300 000 $ или 8 700 000 грн.). Ставка дисконтирования – 11 %.
Доходы от проекта составили:
| Год | Размер дохода, $ |
| 1 | 25000 |
| 2 | 46000 |
| 3 | 60000 |
| 4 | 85000 |
| 5 | 120000 |
Рассчитаем суммы денежных потоков для каждого года:
PV1=25000/(1+0,110)=1 689 225 руб. (22 523 $ или 653 167 грн.);
PV2=46000/(1+0,110)=3 108 075 руб. (41 441 $ или 1 201 789 грн.);
PV3=60000/(1+0,110)=4 054 050 руб. (54 054 $ или 1 567 566 грн.);
PV4=85000/(1+0,110)=5 743 275 руб. (76 577 $ или 2 220 733 грн.);
PV5=120000/(1+0,110)=8 108 100 руб. (108 108 $ или 3 135 132 грн.).
\[ D=\frac{1*22523+2*41441+3*54054+4*76577+5*108108}{22523+41441+54054+76577+108108}=3,68 г. \]
Таким образом, проект окупится на четвертом году.
Чтобы рассчитать дюрацию кредита, можно взять любой график аннуитетных платежей и складывать их суммы до тех пор, пока значение не будет равно телу кредита. Срок платежа, в котором сумма выплаченных заемщиком средств достигнет размера основного долга, и будет искомым значением. При этом банк при определении этого срока учитывает инфляцию и ожидаемую прибыль.
Что такое дюрация простыми словами
Если говорить простым языком, то дюрация – это величина, которая связывает текущую стоимость облигации и купонный доход до ее погашения. Это некий период, за который кредитор сможет вернуть вложенные деньги. В большинстве случаев дюрация обозначается именно в днях.
Для чего нужна и где используется
Чтобы понять, для чего нужна дюрация, предлагаю погрузиться в следующую ситуацию.
Успей воспользоваться удвоением налогового вычета до 31 декабря 2022 г.
Предположу, что у меня есть два возможных заемщика, каждый из них хочет взять кредит на год в размере 1000 руб. Но у меня только одна тысяча, поэтому мне придется выбирать.
- Первый предлагает мне 10 % годовых, но при этом проценты собирается выплачивать каждый месяц, т.е. платежами по 8,3 (3) руб.
- Второй предлагает вернуть мне деньги с большей доходностью, например 11 %, но собирается отдать всю сумму в конце периода через год.
У меня как инвестора возникает мысль, что если я буду получать по 8,3 (3) руб., то могу на них каждый раз покупать ОФЗ, по которым я буду получать 8 % годовых. Значит, после первого платежа я купил облигации на 8,3 (3) руб., мне на них пошли проценты, после второго платежа то же самое и т.д.
Вычисления непростые, поэтому поверьте на слово: на первом заемщике я смогу заработать около 10,366 %, а от второго получу 11 %. Выходит, что 2-й вариант для меня предпочтительнее, но разница не так велика, как казалось изначально.
Так вот дюрация нужна для того, чтобы не вычислять все это самому, а моментально видеть, как бумаги с совершенно разными условиями, сроками и рисками приводятся к общему знаменателю.
Где смотреть
В основном облигации торгуются через российских брокеров. Просматривать и анализировать величины дюрации удобнее всего через торговый терминал, предоставляемый финансовым агентом.
Если нет возможности подключиться к брокерским программам, то необходимые материалы можно также найти в интернете на специализированных сайтах. Доступ к некоторым платный, но есть и свободные ресурсы.
Свойства дюрации
Обобщим основные свойства дюрации облигаций:
- Для облигаций с купоном дюрация всегда меньше их срока жизни. Простыми словами, ценная бумага должна окупить себя до установленного срока погашения.
- Для бескупонных облигаций дюрация равна сроку погашения.
- Цена обязательства увеличивается с уменьшением купонных выплат. И наоборот, если купонные выплаты повышаются, падает рыночная стоимость ценной бумаги.
- Облигация с большей дюрацией имеет более высокий уровень процентного риска.
Понятие и значение для выбора облигаций
Дюрация (англ. duration – длительность) – это период до полного возврата вложенных в покупку облигации средств. Измеряется в годах, но на российских ресурсах чаще можно увидеть единицу измерения в днях.
Полная информация об актуальных стратегиях, которые уже принесли миллионы пассивного дохода инвесторам
В описании облигации отдельно есть параметр “срок до погашения” и отдельно “дюрация”. Вроде бы и первый, и второй показывает, сколько осталось времени до возврата денег. Но цифры не всегда совпадают. Если в первом случае это простой срок до погашения, то во втором – с учетом купонов, амортизации, оферты.
В банковской терминологии есть термин “эффективная процентная ставка”, т. е. ставка с учетом капитализации процентов. Слово “эффективный” можно применить и к сроку возврата денег по облигации, т. к. он тоже учитывает разные характеристики ценной бумаги.
Формулу расчета в буквенном изображении я не буду приводить, чтобы не спугнуть начинающих инвесторов и не отбить у них желания покупать долговые ценные бумаги. Вам не придется по ней считать эффективный срок. Есть специальные ресурсы, где все уже подсчитано. О них поговорим отдельно в статье.
Но для понимания показателя предложу вам упрощенный вариант формулы в текстовом виде:
Дюрация (Д) = Сумма выплат (купоны или погашение номинала) * Время выплаты / Сумму выплат
Пример. Есть две облигации А и Б с одинаковой доходностью 5 % годовых. Номинал у обеих – 1 000 ₽. Срок до погашения – 3 года. У бумаги А купоны выплачиваются 1 раз в год. У бумаги Б – в конце срока вместе с погашением номинала. Денежные потоки по годам приведены в таблице.
| Срок | Погашение номинала | Выплата купона |
| А | ||
| 1 | 50 | |
| 2 | 50 | |
| 3 | 1 000 | 50 |
| Итого | 1 000 | 150 |
| Б | ||
| 1 | ||
| 2 | ||
| 3 | 1 000 | 150 |
| Итого | 1 000 | 150 |
Д (А) = (50 * 1 + 50 * 2 + 1050 * 3) / 1 150 = 2,87 года
Д (Б) = 1 150 * 3 / 1 150 = 3 года
Дюрация в первом случае меньше за счет более частых выплат купонов. Следовательно, меньше и риск. Инвестор быстрее получает возврат средств. Деньги можно опять пустить в инвестиции и заработать. А дюрация бескупонной облигации равна сроку погашения.
При прочих равных условиях лучше выбирать бумаги с меньшей дюрацией, т. к. меньше риск потери капитала. Кроме того, дюрация показывает не только средний срок возврата денег, но и зависимость цены облигации от изменения ключевой ставки Центробанка. Об этом мы тоже еще поговорим.
Можно проследить определенные свойства дюрации. Она применяется для сравнения долговых бумаг между собой и учитывает 4 основных фактора:
- Срок до погашения. Чем больше срок до погашения, тем выше дюрация.
- Амортизация. У долгового инструмента с амортизацией при прочих равных условиях дюрация ниже.
- Размер и периодичность выплаты купонов. Чем больше размер купона и чаще выплаты, тем ниже дюрация.
- Влияние изменения ключевой ставки Центробанка на цену облигации тем ниже, чем меньше срок до погашения и ниже дюрация.
Более 100 крутых уроков, тестов и тренажеров для развития мозга
Начать развиваться
Эффективный срок возврата рассчитывают только для бумаг с постоянным купоном, когда известно, в какие сроки и в каком размере будут выплаты.
Можно провести аналогию с банками. Погашение по кредиту они требуют с заемщиков проводить ежемесячно, тем самым снижают эффективный срок возврата долга за счет более частых платежей и, соответственно, уменьшают свои риски.
Что такое «выпуклость» облигации
Мы уже знаем, что дюрация облигации определяет риск изменения рыночной стоимости в зависимости от размера денежных потоков.
Если имеются две ценные бумаги с одинаковым рассчитанным сроком окупаемости, тогда инвестор обращает внимание на показатель второго порядка – выпуклость облигации, т.е. чувствительность рыночной цены к изменению размера процентных ставок.
Если изменение ставок оказывает существенное влияние на волатильность облигаций, то такая бумага отличается негативной выпуклостью. И наоборот, менее чувствительные к изменению ставок обязательства имеют позитивную выпуклость и низкий уровень риска.
Для чего нужна?
С помощью дюрации инвесторы и аналитики измеряют средний срок возврата инвестиций. Дюрация также помогает понять, насколько чувствительна актуальная цена облигации к изменению ключевой ставки ― это важно учитывать при покупке облигации.
При одинаковой доходности, нужно выбирать облигации с меньшей дюрацией.
Цены облигаций и процентные ставки двигаются в противоположных направлениях (вспоминаем качели): если одна сторона взмывает вверх, другая падает вниз (и наоборот). Облигации с большой (длительной) дюрацией являются более чувствствительными к скачкам процентов.
Таким образом, дюрация – это показатель риска.
Главное что нужно понять: Чем выше дюрация, тем выше риск для инвестора!
Также дюрация позволяет оценить другие финансовые активы с фиксированными выплатами. Например, банки могут рассчитывать дюрацию кредитов и кредитных портфелей. Но это уже другая история.
Как изменение процентной ставки влияет на цену облигаций
Динамика рыночных цен на облигации во многом зависит от изменения процентных ставок. При этом существует обратная зависимость: при росте ставок рыночная цена снижается, при падении ставок – растет.
Эта зависимость далеко не всегда равнозначна. К примеру, если ставки упали на 5 %, то стоимость ценной бумаги может вырасти на те же 5 %. Если же ставки выросли на 5 % – облигация подешевеет на 4 %.
Решающее влияние на доходность долговых обязательств оказывает ключевая ставка Центробанка. Если размер ключевой ставки вырос, купонные облигации падают в цене. При падении ключевой ставки рыночная стоимость таких ценных бумаг растет.
Формула денежной дюрации (по Маколею) не учитывает изменение ставок. Для расчета срока окупаемости инвестиций при переменных ставках лучше использовать показатели эффективной дюрации и модифицированной дюрации облигаций.
Дюрация. Что это такое и почему она важна
Когда разговор заходит о долговых инструментах часто можно встретить такой термин, как дюрация. В обзоре мы разберем, что обозначает этот показатель и как его применять на практике.
При покупке облигации инвестор берет на себя два ключевых риска: кредитный — риск дефолта эмитента, и процентный — риск колебаний рыночной стоимости бумаги в ответ на изменение уровня процентных ставок в экономике.
Пример процентного риска: Есть облигация с фиксированным купоном, торгуемая по номиналу 100% с доходностью 8% в год. Из-за изменения ситуации на рынке, доходность по аналогичным инструментам выросла до 10%. Соответственно, чтобы наша бумага была интересна инвесторам, она должна обеспечивать аналогичную доходность. Но так как купон уже был ранее зафиксирован на уровне 8%, то такая доходность может быть обеспечена только за счет снижения стоимости покупки облигации. Рыночная цена бумаги снижается и становится меньше номинала. В этом и заключается процентный риск облигаций — их цена падает при росте доходностей на рынке и, наоборот, растет в случае их снижения.
Для измерения и сравнения между собой процентных рисков разных долговых бумаг и был веден показатель дюрации.
Как измерить уровень процентного риска
Первым ключевым фактором, который влияет на процентный риск, является срок до погашения.
Пример: есть две абсолютно одинаковые облигации с погашением через 3 года и 5 лет. Из-за роста ключевой ставки на 1% доходности по таким облигациям на рынке также выросли на 1%. Соответственно, компенсировать разницу в доходности к погашению, 3-летняя облигация должна торговаться на 1%*3 года = 3% ниже своей начальной стоимости, 5-летняя бумага — на 1%*5 лет = 5%.
Пример является упрощенным, но наглядно показывает, как соотносится процентный риск со сроком до погашения. Однако помимо срока до погашения имеет значение и размер купона. При прочих равных более привлекательными для инвесторов будут бумаги с большим размером купона. Это значит, что облигация с купоном 20% в случае роста ставок меньше просядет в цене, чем облигация с купоном 10% при одинаковом сроке до погашения.
В 1938 г. Фредерик Маколей разработал свой метод, как учитывать купоны при оценке процентного риска. Он предложил сравнивать облигации не по сроку до погашения, а по средневзвешенному сроку до получения купонов и номинала.
В формуле Маколея каждый платеж по облигации получает свой вес в зависимости от срока, когда он будет получен по методу дисконтирования: чем раньше поступает платеж, тем выше его вес. Сумма взвешенных платежей делится на текущую рыночную цену и получается искомый результат. Новый показатель Маколей предложил называть дюрацией (от англ. duration — длительность).
где: P — текущая цена облигации;
r — доходность к погашению/оферте;
t — срок поступления платежа (купона или номинала);
N — номинал облигации (в деньгах);
C — купонный платеж;
n — количество платежей.
Дюрация Маколея является базовой для расчетов других показателей, связанных с волатильностью цены облигаций. Так как она представляет из себя временной период, она может измеряться в днях. Именно в таком виде ее можно увидеть в терминале QUIK.
Чем выше дюрация облигационного выпуска, тем сильнее он реагирует на изменение требуемой доходности. Иными словами, чем выше дюрация, тем выше процентный риск.
Стоит отметить ряд особенностей, характерных для дюрации:
— При прочих равных, чем больше срок до погашения, тем выше дюрация.
— При прочих равных, чем выше величина купона и чем чаще он выплачивается, тем ниже дюрация.
— При прочих равных, чем выше доходность к погашению, тем ниже дюрация.
— Дюрация Маколея бескупонной облигации равна сроку до погашения.
Применение на практике
На практике обычно используется модифицированная дюрация (МД), которая рассчитывается на основе дюрации Маколея по простой формуле:
Учитывая, что в QUIK дюрация Маколея измеряется в днях, полученное значение необходимо разделить еще на 365. Для примера рассчитаем МД для выпуска ОФЗ-ПД 25083 по показателям из таблицы на предыдущей картинке. Получим 1092 / ((1+ 0,0821)*365) = 2,76.
Модифицированная дюрация является безразмерной величиной, а ее математический смысл заключается в следующем: модифицированная дюрация является приближенным изменением стоимости облигации в ответ на изменение доходности на 1% (100 базисных пунктов).
ΔP = -МД * Δy,
где ΔP — изменение стоимости облигации, Δy — изменение доходности.
По этой формуле можно оценить изменение стоимости облигации при небольших изменениях доходности.
Пример: Облигация с номиналом 1000 руб. торгуется по цене 101,7% (1017 руб.), с доходностью 8% и модифицированной дюрацией 1,72. Если доходности на рынке вырастут с 8% до 10%, то стоимость облигации изменится примерно на -1,72 * (0,1-0,08) = -0,0344 = -3,44%. Бумага будет торговаться по цене 1017 * (1- 0,0344) = 982,02 руб. (98,2% от номинала)
Модифицированная дюрация облигационного портфеля из нескольких бумаг упрощенно рассчитывается, как сумма произведений дюрации каждого выпуска на его долю:
Пример: составлен портфель из двух бумаг. Доля первой бумаги 30%, ее дюрация 0,8. Доля второй бумаги 70%, дюрация 1,4. Дюрация всего портфеля будет равна 0,3*0,8 + 0,7*1,4 = 1,22.
При формировании портфеля дюрация используется согласно следующей стратегии:
Если ожидается снижение уровня процентных ставок, то инвестору стоит повысить дюрацию портфеля, чтобы извлечь большую прибыль из-за роста цен.
Если ожидается рост процентных ставок, то стоит снизить дюрацию портфеля, чтобы сократить потери от снижения цен.
Если у вас нет сформированного мнения о будущей динамике процентных ставок, формируйте портфель так, чтобы его дюрация была примерно равна сроку предполагаемого инвестирования.
Важный момент: дюрация в терминале QUIK учитывает дюрацию по облигациям с переменным купоном до даты ближайшей оферты put. Но оферта call в терминале не учитывается. Дюрацию до оферты call можно рассчитать самостоятельно по формуле, либо посмотреть на специализированных ресурсах типа cbonds.ru и rusbonds.ru.
Выпуклость
Для обычного частного инвестора объем приведенный выше информации вполне достаточен, чтобы управлять процентным риском небольшого портфеля, используя дюрацию. Но для более точных расчетов, важность которых возрастает с ростом суммы и сроков инвестиций, необходимо познакомиться еще с одним понятием.
Как было указано ранее, модифицированная дюрация дает только приблизительную оценку и подходит лишь для небольших изменений доходности. Все дело в том, что зависимость цены облигации от ее доходности не линейная, а представляет из себя кривую:
Таким образом, чем больше изменение процентной ставки, тем больше реальное изменение стоимости будет отклоняться от расчетного. Диапазон ставок, в котором погрешность можно считать несущественной, зависит от параметров конкретной облигации и объема средств, которые планируется в нее инвестировать.
Вторым важным моментом является несимметричность графика Цена/Доходность. При снижении процентной ставки на 1% цена вырастет больше, чем снизится при аналогичном росте ставки на 1%.
Для того чтобы снизить погрешность вычислений используют еще один параметр, характеризующий выпуклость кривой Цена/Доходность. Его так и называют выпуклость, или еще используется термин конвекция.
Математический смысл выпуклости выходит за рамки этой статьи, но для практического применения обычному частному инвестору он, в общем-то, ни к чему. Значение выпуклости можно найти на тех же специализированных ресурсах вроде rusbonds.ru или cbonds.ru. В расчеты выпуклость (Впкл) включается следующим образом:
Первое слагаемое этой формулы, которое вы уже видели ранее, называется процентное изменение цены, обусловленное дюрацией. Второе слагаемое, соответственно, процентное изменение цены, обусловленное выпуклостью.
Второе слагаемое корректирует рассчитанное по дюрации значение и вносит в него несимметричность. Положительная выпуклость, характерная для обыкновенных облигаций, корректирует результат в сторону роста цены и является позитивным моментом для инвестора.
Одновременное использование дюрации и выпуклости дает более корректное значение изменения доходности облигации в ответ на смещение процентных ставок.
При прочих равных большая выпуклость более выгодна для инвестора.
На графике хорошо видно, что при одинаковой дюрации более выпуклая облигация B оказывается выгоднее для инвестора при значительном изменении процентных ставок. При снижении ставок она быстрее растет в цене, а при их росте — медленнее теряет свою стоимость.
В случае если инвесторы на рынке ожидают высокой волатильности процентных ставок, участники рынка могут предпочитать среди бумаг с одинаковой дюрацией те, у которых более высокая выпуклость. Это будет отображаться в виде меньшей доходности таких облигаций.
И напротив, когда ожидается низкая волатильность ставок, инвесторам незачем жертвовать доходностью ради выпуклости и они переводят капитал в более доходные бумаги. Эту закономерность частный инвестор может использовать в качестве индикатора настроений на долговом рынке.
Выпуклость всего портфеля облигаций измеряется аналогично дюрации портфеля: выпуклость каждой бумаги умножается на её вес в портфеле и полученные значения складываются.
Особенности применения дюрации
Может возникнуть закономерный вопрос: почему бы вместо дюрации и выпуклости просто не использовать функцию Цена = f (доходность). Однако такие расчеты оказываются чересчур громоздкими даже при использовании вычислительной техники. Очень часто дюрация и выпуклость дают возможность получить хорошее приближение искомой величины с допустимым уровнем погрешности.
Приведенные показатели дюрации и выпуклости справедливы только для обыкновенных облигаций без встроенных опционов. Если изменение доходностей приводит к изменениям предполагаемых денежных потоков облигации, то меры дюрации и выпуклости применимы лишь в некоторых специфических случаях.
Понятие дюрации и оценка процентного риска долговых бумаг в целом не ограничивается приведенными в данном обзоре показателями. Однако для обычного частного инвестора этих понятий достаточно, чтобы разумно сформировать портфель облигаций с учетом процентного риска. В том случае если вы хотите еще глубже вникнуть в методики управления облигационным портфелем, рекомендуем ознакомиться со специализированной литературой, например, Фрэнк Фабоцци «Рынок облигаций. Анализ и стратегии».
Открыть счет
БКС Брокер
Пример определения дюрации
Рассмотрим пример, в котором рассчитаем дюрацию для «смешанного» портфеля, включающего купонные и бескупонные ОФЗ, а также корпоративные бумаги.
Итак, портфель инвестора выглядит следующим образом:
| Наименование ценной бумаги | Номинальная стоимость, $ | Рыночная цена, $ | Срок до погашения, лет | Купон, % | Количество выплат в год | Дюрация, лет | Доля в портфеле, % |
| ОФЗ | |||||||
| 1 | 12,5 | 12,6 | 6 | 7,75 | 2 | 0,07 | 5 |
| 2 | 12,5 | 13 | 7 | 11 | 3 | 0,07 | 5 |
| 3 | 12,5 | 11 | 2 | 2 | 10 | ||
| 4 | 12,5 | 14 | 9 | 10 | 1 | 0,16 | 10 |
| 5 | 12,5 | 17 | 10 | 9 | 3 | 0,04 | 10 |
| Корпоративные | |||||||
| ВЭБ | 12,5 | 12,5 | 5 | 11,6 | 1 | 0,30 | 10 |
| Газпром | 12,5 | 10,6 | 4 | 7,7 | 2 | 0,09 | 10 |
| Рольф | 12,5 | 11,5 | 2 | 9 | 4 | 0,09 | 10 |
| РЕСО-Лизинг | 12,5 | 12,3 | 2 | 9,7 | 2 | 0,18 | 10 |
| Гарант-Инвест | 12,5 | 11,2 | 2 | 13,5 | 4 | 0,12 | 10 |
| Тинькофф | 12,5 | 12,9 | 2 | 7,3 | 2 | 0,16 | 10 |
Мы видим, что все ценные бумаги, за исключением бескупонных, окупятся в первом году после приобретения. Следовательно, портфель состоит из низкорисковых облигаций.
По приведенной выше формуле рассчитаем дюрацию по портфелю и получим значение 0,14.
Дюрация Маколея: формула расчёта
Наиболее известный способ расчета дюрации — формула Маколея. Дюрация Маколея – это средневзвешенное время до получения купонов и номинала. Дюрация Маколея измеряется в годах.
В формуле Маколея каждый платеж по облигации получает свой вес в зависимости от срока, когда он будет получен по методу дисконтирования: чем раньше поступает платеж, тем выше его вес. Сумма взвешенных платежей делится на текущую рыночную цену и получается искомый результат.
Формула является довольно сложной и запутанной, поэтому обычные инвесторы к самостоятельным расчетам по ней прибегают крайне редко, предпочитая использовать специальные сервисы с готовыми значениями по каждому виду облигаций. Как раз это значение можно увидеть в терминале в QUIK.
Упрощенное объяснение формулы:
В числителе: Сумма из (поступление по облигации * время поступления) Знаменатель: Цена облигации + НКД
Поступления по облигациям – это все будущие платежи: купоны и погашение. Так как это будущие платежи разного времени, нужно каким-то образом привести их к сегодняшнему дню. С точки зрения математики, эти платежи надо освободить от доходности, то есть дисконтировать. Это делается потому, что 1000 рублей сейчас НЕ РАВНЫ этой сумме через 1 год, через 2 и т.п. Дисконтирование — это процесс, обратный начислению процентов.
Более важно просто понимать, что дюрация облигаций зависит от цены и оставшегося до погашения срока, при этом:
- При неизменной цене, если срок до погашения уменьшается, дюрация тоже уменьшается.
- При неизменном сроке, если цена на облигацию вырастает, то дюрация тоже уменьшается; если же цена снижается, то увеличивается.
Таким образом, дюрация облигаций постоянно меняется, она пересчитывается каждый день и каждый день будет разной.
Как применять дюрацию на практике
Итак, обобщим понятие дюрации простыми словами, чтобы было понятно даже для детей: мы даем деньги в долг под процент и нам нужно знать, как скоро мы сможем вернуть свои средства так, чтобы не остаться в убытке. Понятно, что давая деньги в долг человеку под проценты или без них, мы всегда принимаем риск невозврата средств или просрочки.
В случае с ценными бумагами такой риск тоже имеется, но долговые бумаги имеют свой плюс: их можно продать до срока погашения по текущей рыночной цене.
Если вы приобретаете облигации и держите их до погашения, дюрация вам не особо и нужна. Но если вы являетесь трейдером, она вам необходима. Конечно, самостоятельно рассчитывать срок окупаемости бумаги по сложной формуле не нужно, т.к. это займет много времени и велика вероятность ошибки. Можно использовать специальные онлайн-сервисы и торговые терминалы.
Как узнать дюрацию
Считать самостоятельно ничего не нужно. Посмотреть значение дюрации обычно можно в сервисах с калькулятором доходности облигаций. Это поможет принять взвешенное решение относительно инвестиций в те или иные облигации.
Найти калькулятор доходности облигаций можно здесь:
- Калькулятор облигаций на rusbonds.
- Калькулятор на сайте мосбиржи.
- На smart-lab.
- cbonds.ru (платные инструменты).
Значение дюрации также есть в торговом терминале QUIK.
Рассмотрим на первом примере.
Как использовать калькулятор:
- перейдя на страницу сайта, из выпадающего списка «Наименование» необходимо выбрать нужную облигацию, подходящую по доходности;
- в поле «Расчет по цене» — «Чистая цена» вводим рыночную цену на данный момент, которая есть сейчас;
- нажимаем кнопку «Рассчитать».
Ещё значение дюрации можно посмотреть на сайте rusbonds на страницах облигаций во вкладке «Доходность».
Взаимосвязь выпуклости и дюрации
Если инвестор графически представит получение доходности от облигаций, то получит не прямую линию, а выпуклую кривую, изгиб или «выпуклость» которой зависит от доходности ценной бумаги.
Понятие «выпуклость» — это финансовый термин и характеризуют зависимость стоимости облигации от ее доходности. «Выпуклость» напрямую связана с дюрацией и отражает свойство ее изменения – чем больше скорость изменения, тем сильнее изменяется дюрация.
График выпуклости выглядит следующим образом:
Для инвестора значение «выпуклости» говорит о том, что чем больше выпуклость конкретной облигации, тем быстрее растет доходность, но и тем ниже становится стоимость облигации.
Дюрация облигации: расчет, формула
Величина дюрации может быть использована для характеристики многих инвестиционных инструментов, но чаще всего ее применяют для учета рисков при использовании ценных бумаг с установленным сроком обращения.
Наиболее распространенным использованием показателя дюрации является расчет дюрации облигации. Как уже было приведено выше, дюрация облигации идентична общему понятию дюрации, что представляет собой определенное количество лет, необходимое на погашение полной стоимости облигации.
Облигация является эмиссионной долговой ценной бумагой и ее рыночная стоимость может меняться в течение периода ее полного погашения.
Дюрация позволяет инвестору в полной мере оценить финансовую привлекательность облигаций на рынке ценных бумаг, учитывая сразу несколько важных показателей — срок, на который выдана облигация, ставку процента (купон), номинальную стоимость ценной бумаги. Вычисленный показатель дюрации облигации поможет инвесторам принять решение о размещении портфеля ценных бумаг с наибольшей прибылью.
Расчет дюрации ценной бумаги может быть произведен несколькими способами:
Формула дюрации — как подсчитать значение
Дюрация зависит от трех составляющих: цена, процентная ставка и срока до погашения
De = [ Pi- + Pi+ ] / [Pr &timex; (i+ — i—) ]
Где:
- De – значение эффективной дюрации облигации
- Pi- – рыночная цена при понижении ставки
- Pi+ – рыночная цена при возрастании ставки
- Pr – номинальная цена ценной бумаги
- i+ – повышенная стартовая ставка
- i— – сниженная стартовая ставка
Считать самостоятельно дюрацию облигации по формуле не нужно. Она уже подсчитана автоматически. Данные можно посмотреть в торговом терминале QUIK или в открытых источниках по облигациям: https://www.rusbonds.ru (например).
Сложность формулы заключается в том, что текущие деньги не равны завтрашним деньгам. Поэтому для точности расчётов их следует дисконтировать.
Есть также другая формула дюрации, которая учитывает еще и ставку дисконтирования:
D = [ ( [∑ t × C] / (1+i)t) + ( / (1+i)n)] / p
Где:
- n – число платежей
- t – период, требуемый для полного погашения
- M – погашение номинальной цены облигации
- C – денежные поступления процентной прибыли
- i – ставка дисконтирования
- p – рыночная цена облигации
Дюрация Маколея
Фредерик Маколей вывел формулу вычисления дюрации еще в 30-х годах прошлого столетия, однако практическое использование в России ее началось только с 1993 г.
Формула выглядит следующим образом:
- где D – дюрация,
- n – количество платежей,
- t – время, необходимое для полного погашения,
- M – погашение номинальной стоимости ценной бумаги,
- С – денежный поток процентных доходов,
- i – ставка дисконтирования,
- p – рыночная стоимость ценной бумаги
К примеру, инвестор имеет две облигации номинальной стоимостью 5000 рублей каждая, при этом одна из них с нулевым купоном (бескупонная) и сроком погашения 3 года, другая с купоном, равным 5 %, который выплачивается ежегодно, сроком погашения также 3 года.
В первом случае дюрация будет равна сроку погашения облигации, а именно 3 года, так как денежный поток процентных доходов равен 0.
Во втором случае расчет можно произвести следующим образом:
Дюрация облигации с 5 % купоном составит 2,86 года.
Модифицированная дюрация
В случае если процентная ставка доходности меняется в каком-либо временном промежутке до момента полного погашения номинальной стоимости, то необходимо использовать для расчета формулу модифицированной дюрации:
Dm= D/(1+ Cm/n)
- где Dm – модифицированная дюрация,
- Cm – доходность до погашения,
- n – количество выплат по купонам в год
Применяя предыдущий расчет, вычислим Dm= 2.86/((1+0.05/1))=2.86/1.05=2.72
Таким образом, при увеличении дохода по купону, дюрация снижается.
Однако, модифицированная дюрация применима лишь в том случае, если доходные денежные потоки с изменением процентной ставки не меняются, что в практическом применении чаще всего невозможно. Для расчета необходим более чувствительный инструмент к колебаниям ставки процента и, соответственно, доходности, каким и является эффективная дюрация.
Эффективная дюрация
При расчете эффективной дюрации облигации учитываются колебания процентных ставок как в сторону уменьшения, так и в сторону увеличения. Формула для расчета выглядит следующим образом:
- Где De – эффективная дюрация,
- Pi- — стоимость облигации при уменьшении процентной ставки,
- Pi+ — стоимость облигации при увеличении процентной ставки,
- Ро – начальная стоимость облигации,
- i+ — увеличенная начальная процентная ставка,
- i- — уменьшенная начальная процентная ставка.
Расчет эффективной дюрации применим с использование биноминального процентного дерева для исчисления стоимости облигации с учетом колебаний процентных ставок.
Пример расчета дюрации
Смоделируем схемы расчета ДО по двум видам похожих инструментов. Для этого сравним ОФЗ номиналом по 1 тыс. руб. Срок выкупа – 12 месяцев. Прибыльность – 10%. Сумма выплат за год – 100 р. Отличается только периодичность денежных поступлений:
- Купоны выдаются 2 раза в год. Стоимость купона – 50 р.
- Выплаты делаются ежеквартально (4 раза за год). Цена купона – 25 р.
В таблице указаны основные параметры инструментов:
| Показатель | №1 | №2 |
| Номинал, руб. | 1 000 | 1 000 |
| Размер купона, в руб. | 50 | 25 |
| Количество выплат | 2 | 4 |
| График платежей | — | — |
| 01.04.2020 | — | 25 |
| 01.07.2020 | 50 | 25 |
| 01.10.2020 | 25 | |
| 01.01.2021 | 50 | 25 |
| Сумма выкупа, руб. | 1 100 | 1 100 |
Формула расчета №1:
Общее количество дней дюрации составляет менее 1 года. Расчеты делались на основании годовых показателей, но без учета дисконтирования. Это упростило задачу и не отразилось на конечном результате.
Формула расчета №2:
Значение во втором примере немного меньше. Причина – более быстрый возврат купонных выплат. Стоимость финансового инструмента окупится быстрее.
Инвестору выгоднее выбирать ОФЗ с меньшей ДО. Это позволит снизить риски и обеспечит активное движение капитала. Следовательно, инвестор получит большую прибыль за счет повторного вложения средств.
Повышенный риск присущ и бескупонным облигациям. По ним нет промежуточных платежей. Выплата дохода делается единовременно.
По эмиссии облигаций с определенным до даты выкупа денежным потоком дюрация рассчитывается к погашению. По выпуску бумаг с неисполненными офертами и частично определенным денежным потоком показатель рассчитывается к оферте.
Бессрочные облигации
Бессрочная облигация подходит вкладчикам, которые хотят довольно долго получать стабильную прибыль. Бумага не предусматривает выкуп номинала. Ее владельцу полагается только купонная прибыль. Но в условиях эмиссии может быть сказано, что ДО имеет определенный срок. Например, принудительное погашение (колл-опцион) ОФЗ (КО) производится спустя 10 лет.
Первое размещение вечных облигаций на Мосбирже провел ВТБ банк в 2012 году. Позже на рынок вышел Газпромбанк и Промсвязьбанк. В 2016 году финансовые инструменты начал использовать Альфа-банк и ТКС банк (Тинькофф).
Вечные облигации выпускались в виде евробондов в иностранной валюте. Цена минимального лота начиналась от 100 000 долларов. Купоны вечных облигаций могли быть фиксированными или плавающими. ВТБ банк и Газпромбанк привязывали купонные выплаты к 5 и 10-летним гособлигациям США (+ 7,1 и 8,1% соответственно). Колл-опционы были запланированы на 2022 и 2022 гг.
Рублевые облигации сумел выпустить только Россельхозбанк. С 2018 года на рынок могут выходить не только банки, но и другие финансовые компании.
В 2022 году ОАО «РЖД» разместило евробонды серии 001Б-04 объемом 80 млрд. руб. Ставка купона – 7,25% годовых. По ценным бумагам предусмотрены колл-опционы каждые пять лет. В качестве организаторов выступило несколько организаций – ВТБ Капитал, МКБ, Sberbank CIB, Промсвязьбанк, БК «Регион» и Россельхозбанк.
Бессрочная облигация считается довольно выгодным инструментом вложения денег. Однако бумага не застрахована от всех рисков. При банкротстве компании (эмитента) она не предоставляет заметных выгод своему владельцу.
Облигации с офертой
Сделать верный расчет ДО можно при точно сформированных купонных выплатах. Размер платежа и ставка купона могут отличаться. Однако эти данные должны быть известны впоследствии.
Оферта – предложение о заключении соглашения, адресованное узкому или неограниченному кругу лиц. Договор считается заключенным, как только получатель согласится с его условиями.
Конечно, иногда встречаются облигации, по которым нет данных о будущих выплатах. Например, бумаги с плавающим купоном или КО с безотзывной офертой.
Расчет ДО с плавающим купоном не будет точным. Следовательно, не обеспечит инвестора полезными сведениями. По корпоративным бумагам дюрацию нужно рассчитывать к моменту оферты, приравнивая ее к дате выкупа. Оферту можно рассматривать, как возможность преждевременного выкупа КО. Формула расчета:
Где:
- числитель – разница между ценностью гособлигации на фоне снижения ставки и ее ценой во время роста ставки;
- знаменатель – базовая ценность бумаги, умноженная на разницу между ставками.
Расчеты показывают, что показатель значительно короче времени выкупа. Например, по облигации «ФСК ЕЭС Б4» до обратного выкупа остается 12243 дня, а ДО – 1421 день.
Причина – дюрация рассчитывается по времени к оферте. ДО не бывает больше, чем срок до выкупа бумаги. Максимум – показатель будет равен времени выкупа. Например, если купон выплачивается единовременно или речь идет об ОФЗ (КО) бескупонного типа.
Определение понятия
Простыми словами дюрация облигации (ДО) – количество календарных дней или лет, по истечении которых трейдер в полном объеме возмещает расходы, понесенные при покупке ценной бумаги. Чем ниже показатель, тем короче срок, соответственно, меньше инвестиционный риск.
Значение дюрации зависит от нескольких факторов – типа ценной бумаги, процента купона, периодичности выплат.
Рассмотрим несколько примеров:
- Облигация с купоном 25%. Срок полного погашения бумаги – 5 лет, номинальная цена 50 тыс. рублей, проценты инвестор получает один раз в квартал. Соответственно один раз в 3 месяца поступает 12,5 тыс. рублей и трейдер возвращает вложенные 50 тыс. через год. В таком случае дюрация равна 365 дней.
- Облигация без купона сроком в 5 лет. В данном варианте инвестор получает вложенные средства только через 5 полных лет, дюрация составит 1825 дней.
Из двух примеров видно, что ценная бумага без купона будет более рискованной, так как полный возврат затраченных денежных средств займет больше времени. Чем выше купонный процент, тем ниже дюрация. Если инвестор выбирает вариант без купона, то дюрация – будет полностью соответствовать периоду погашения.
Для более простого понимания можно провести аналогию с кредитованием. Если заемщик производит ежемесячную выплату процентов, то банк несет меньший риск, получая деньги с первого месяца. В том случае, когда возврат займа и процентов приходится на последний день договора, риск намного выше, а период возврата вложения – больше.
Важно! Дюрация облигаций с купонным доходом всегда ниже, чем по бескупонным ценным бумагам.
Подробнее: о купонных облигациях.