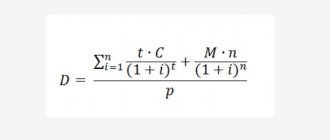The duration of a bond is the period after which an investor will be able to fully recoup their initial investment. It is calculated using a fairly complex formula, which is not necessary to memorize. It is only important to understand that duration is calculated in years or days and is determined by calculating the weighted average.
The main indicator that characterizes duration is interest rate risk. An investor who has debt in their portfolio needs to have a basic understanding of how bond duration is calculated. You can use various online services for calculations.
In this article we will analyze what bond duration is in simple words, provide formulas and calculate this indicator using examples.
Why is it needed and where is it used?
So, the duration of a bond is the payback period for investments in a security. For a zero coupon bond, this value is equal to the life of the debt obligation. We will consider in detail the duration of a coupon bond and first give the basic definitions that we will need.
A bond is a debt obligation of the state or company, under which the issuer (borrower) undertakes to return to the acquirer (lender) the face value of the security plus interest (coupon) within a certain period.
A coupon is the reward on a bond, expressed as a percentage of its face value.
Accumulated coupon income (ACI) is the sum of all coupon payments. Such payments can be made at different intervals:
- annually;
- semiannually;
- quarterly.
The more often payments are made, the more complex the calculation of duration.
The discount rate is a percentage of the expected future profit.
In addition to bonds, duration is also used to calculate the payback period of portfolios, loans and other debt obligations, and investment projects. Using this indicator, you can calculate the repayment period of the debt by the creditor.
The essence in simple words
Duration is when the coupon payments pay off the cost of purchasing the bond. The payback period takes into account all coupon payments paid at different times and various features of the bond, such as amortization or call. If there are no coupon payments, amortization, or put option, then the duration coincides with the maturity of the bond.
The bottom line. Very simplified, but the meaning is something like this. When you buy a bond, you pay its market value. Market value is indicated as a percentage of face value. Let our bond be worth 101%. With a nominal value of 1000 rubles, we will buy it for 1010 rubles. She brings us 50 rubles a year. Let's say it matures in 50 years. This means it will pay off earlier due to coupons: 1010/50 = 20.2 . Those. in about 20 years - this is duration.
The longer the time until maturity, the longer the duration: the investor will take longer to return his money. And vice versa: if coupon payments are larger and more frequent, and the time until maturity is short, then the duration will be less because the investor will get his money back faster.
If you imagine that the expected payments are money bags placed on a children's swing, then:
- the distances between them are the intervals between payments;
- the size of the bags is the volume of funds paid (the largest one is the last cash flow);
- the number of bills in them is the cost of each payment.
In order to balance the swing, on which there is a certain number of bags and one large “trunk” with money, we must choose an equilibrium point. The duration indicator in this model will be the distance from the found point to the beginning of the swing.
Effective duration and offer
A more accurate formula is the effective duration of bonds, which takes into account changes in the interest rate both up and down. This formula is suitable for bonds with an offer, for which there is an option to repurchase before maturity.
\[ D_e=\frac{P_{i-} – P_{i+}}{P_0*(i_+ – i_-)} , where \]
\( P_{i-} \) - market price in case of a rate decrease;
\( P_{i+} \)- market price in case of rate increases;
\( P_0 \)– initial price;
\( i_+ \)- size of the increased bet;
\( i_- \) - the size of the reduced rate.
Let's assume that the rate can change by 2% up and 3% down. Then, using the previous calculations, we get:
\( P_{i+} \)=25-(25*1.39*2/100)=1,826 rub. ($24.34 or 706 UAH);
\( P_{i-} \)=25+(25*1.39*3/100)=1,953 rub. ($26.04 or 755 UAH);
\( i_+ \)= 12%;
\( i_- \)= 7%.
\[ D_e=\frac{26.04-24.34}{25*(12-7)}=0.01 \]
A value close to zero indicates low sensitivity of the market value of a debt obligation to changes in interest rates. In simple terms, low duration is an indicator of low risk.
Accordingly, a bond with a longer duration represents higher risk and a longer payback period.
This formula should be used if the government is preparing decisions to change the Central Bank rate.
Summary
Duration comes from the English. duration (translated as “duration”) and means the period required to return the funds invested in the bond, taking into account the size and frequency of coupon payments. Duration is a time characteristic, so it is measured in days/years and changes daily.
Duration is used when comparing bonds. Bonds with shorter duration are considered more reliable.
The lower the duration, the less the impact of interest rate changes. To understand how a bond's price will change when interest rates change, use the basis point value.
If interest rates are expected to rise, then bonds with a shorter duration are preferable; if a decrease, bonds with a longer duration are preferable.
I hope that after reading this article you will understand such a bond parameter as duration, which many novice investors have difficulty understanding, and you will not have any difficulties in choosing the right bonds to buy.
Bond portfolio duration
The duration of the portfolio is calculated by determining the weighted average payback period of the securities included in the portfolio. In this case, their percentage ratio is taken into account.
Example. The investor's portfolio consists of five types of OFZ.
| Bond | D, years | Portfolio share, % |
| 1 | 2,68 | 20 |
| 2 | 1,92 | 20 |
| 3 | 1,89 | 20 |
| 4 | 2,14 | 20 |
| 5 | 2,87 | 20 |
\[ Dport=2.68*0.2+1.92*0.2+1.89*0.2+2.14*0.2+2.87*0.2=2.3 g.\[ ]
Thus, the duration of a portfolio is the average time it takes for an investor to recoup his initial investment.
What needs to be taken into account here is that if rebalancing was carried out before the maturity date, then the duration of the bond portfolio must be calculated again. In this case, the indicator for sold securities should be taken as the actual period of stay in the portfolio. In simple words, if a bond with a maturity of 3 years was sold in 2 years, then its duration will be 2 years. The amount of cash flow should be calculated taking into account the income accrual.
Modified duration
Modified duration is the second way to measure duration. With its help, the investor determines by what percentage the price of the bond will change if interest rates change.
MD = Macaulay Duration / (1 + Interest Rate)
For small changes the following formula works:
Change in price / Market price with accrued income = −MD × Change in rates
Considering that in QUIK the Macaulay duration is measured in days, the resulting value must be divided by another 365.
Modified duration is a dimensionless quantity, and its mathematical meaning is as follows: modified duration is an approximate change in the value of a bond in response to a 1% (100 basis points) change in yield.
For example, MD is 3, the bond price taking into account the cash flow is 95%, the yield to maturity is 8% per annum. We can determine how the price will change if the yield increases by 0.5 percentage points and becomes equal to 8.5%.
X / 0.95 = −3 × 0.005
X = −3 × 0.005 × 0.95 = −0.01425
If yields rise by 0.5%, the bond price will decline by 1.4%.
Project duration
The payback period is determined not only for investments in securities, but also for various business projects.
Example. The company is launching a new business project with an initial investment of RUB 22,500,000. ($300,000 or 8,700,000 UAH). The discount rate is 11%.
Income from the project amounted to:
| Year | Income amount, $ |
| 1 | 25000 |
| 2 | 46000 |
| 3 | 60000 |
| 4 | 85000 |
| 5 | 120000 |
Let's calculate the amount of cash flows for each year:
PV1=25000/(1+0.110)=1,689,225 rubles. ($22,523 or 653,167 UAH);
PV2=46000/(1+0.110)=3,108,075 rub. ($41,441 or 1,201,789 UAH);
PV3=60000/(1+0.110)=4,054,050 rub. ($54,054 or 1,567,566 UAH);
PV4=85000/(1+0.110)=RUB 5,743,275 ($76,577 or UAH 2,220,733);
PV5=120000/(1+0.110)=8,108,100 rub. ($108,108 or 3,135,132 UAH).
\[ D=\frac{1*22523+2*41441+3*54054+4*76577+5*108108}{22523+41441+54054+76577+108108}=3.68 g.\]
Thus, the project will pay off in the fourth year.
To calculate the duration of a loan, you can take any schedule of annuity payments and add their amounts until the value is equal to the body of the loan. The payment period in which the amount of funds paid by the borrower reaches the amount of the principal debt will be the desired value. In this case, the bank takes into account inflation and expected profit when determining this period.
What is duration in simple words
In simple terms, duration is a value that connects the current value of a bond and the coupon income before its maturity. This is a certain period during which the lender will be able to return the invested money. In most cases, duration is indicated in days.
What is it for and where is it used?
To understand why duration is needed, I suggest diving into the following situation.
Hurry up to take advantage of the doubling of the tax deduction until December 31, 2022.
Let's assume that I have two possible borrowers, each of them wants to take out a loan for a year in the amount of 1000 rubles. But I only have one thousand, so I have to choose.
- The first one offers me 10% per annum, but is going to pay interest every month, i.e. in payments of 8.3 (3) rubles.
- The second one offers to return the money to me with a higher yield, for example 11%, but is going to give the entire amount at the end of the period in a year.
As an investor, I have the idea that if I receive 8.3 (3) rubles, I can use them to buy OFZs each time, for which I will receive 8% per annum. This means that after the first payment I bought bonds for 8.3 (3) rubles, I received interest on them, after the second payment the same thing, etc.
The calculations are not easy, so take my word for it: I can earn about 10.366% from the first borrower, and 11% from the second. It turns out that option 2 is preferable for me, but the difference is not as great as it initially seemed.
So, duration is needed in order not to calculate all this yourself, but to instantly see how securities with completely different conditions, terms and risks are brought to a common denominator.
Where to see
Bonds are mainly traded through Russian brokers. The most convenient way to view and analyze duration values is through a trading terminal provided by a financial agent.
If it is not possible to connect to brokerage programs, then the necessary materials can also be found on the Internet on specialized sites. Access to some is paid, but there are also free resources.
Properties of Duration
Let us summarize the main properties of bond duration:
- For bonds with a coupon, the duration is always less than their life. In simple terms, a security must pay for itself before its stated maturity date.
- For zero-coupon bonds, duration is equal to maturity.
- The price of the obligation increases as coupon payments decrease. Conversely, if coupon payments increase, the market value of the security falls.
- A bond with a longer duration has a higher level of interest rate risk.
Concept and implications for bond selection
Duration (English: duration) is the period until the full return of the funds invested in the purchase of a bond. It is measured in years, but on Russian resources you can more often see the unit of measurement in days.
Complete information about current strategies that have already brought millions of passive income to investors
In the description of the bond there is a separate parameter “time to maturity” and a separate “duration” parameter. It seems that both the first and second show how much time is left before the money is returned. But the numbers don't always match. If in the first case this is a simple term until maturity, then in the second - taking into account coupons, depreciation, and offer.
In banking terminology there is the term “effective interest rate”, i.e. the rate taking into account the capitalization of interest. The word “effective” can also be applied to the repayment period of the bond, since it also takes into account the different characteristics of the security.
I will not give the calculation formula in letter form, so as not to frighten novice investors and discourage them from buying debt securities. You don't have to use it to calculate the effective period. There are special resources where everything has already been calculated. We'll talk about them separately in the article.
But to understand the indicator, I will offer you a simplified version of the formula in text form:
Duration (D) = Payment amount (coupons or par redemption) * Payment time / Payment amount
Example. There are two bonds A and B with the same yield of 5% per annum. The denomination for both is 1,000 ₽. The maturity period is 3 years. For paper A, coupons are paid once a year. For paper B - at the end of the term along with the redemption of the par value. Cash flows by year are shown in the table.
| Term | Redemption of par value | Coupon payment |
| A | ||
| 1 | 50 | |
| 2 | 50 | |
| 3 | 1 000 | 50 |
| Total | 1 000 | 150 |
| B | ||
| 1 | ||
| 2 | ||
| 3 | 1 000 | 150 |
| Total | 1 000 | 150 |
D (A) = (50 * 1 + 50 * 2 + 1050 * 3) / 1,150 = 2.87 years
D (B) = 1,150 * 3 / 1,150 = 3 years
Duration in the first case is less due to more frequent coupon payments. Therefore, there is less risk. The investor receives a return on funds faster. The money can be invested again and earned. And the duration of a zero-coupon bond is equal to the maturity date.
All other things being equal, it is better to choose securities with a shorter duration, since there is less risk of capital loss. In addition, duration shows not only the average repayment period, but also the dependence of the bond price on changes in the key rate of the Central Bank. We will also talk about this later.
It is possible to trace certain properties of duration. It is used to compare debt securities with each other and takes into account 4 main factors:
- Time to maturity. The longer the term to maturity, the higher the duration.
- Depreciation. A debt instrument with amortization, other things being equal, has a lower duration.
- Amount and frequency of coupon payment. The larger the coupon size and the more frequent the payments, the lower the duration.
- The impact of a change in the Central Bank's key rate on the price of a bond is lower, the shorter the maturity and the lower the duration.
More than 100 cool lessons, tests and exercises for brain development
Start developing
The effective return period is calculated only for securities with a constant coupon, when it is known when and in what amount the payments will be made.
An analogy can be drawn with banks. They require borrowers to repay the loan monthly, thereby reducing the effective repayment period due to more frequent payments and, accordingly, reducing their risks.
What is the "convexity" of a bond?
We already know that the duration of a bond determines the risk of changes in market value depending on the size of cash flows.
If there are two securities with the same calculated payback period, then the investor pays attention to the second-order indicator - the convexity of the bond, i.e. sensitivity of market price to changes in interest rates.
If changes in rates have a significant impact on the volatility of a bond, then such a security is characterized by negative convexity. Conversely, liabilities that are less sensitive to changes in rates have positive convexity and a low level of risk.
What is it for?
Duration is used by investors and analysts to measure the average return on an investment. Duration also helps to understand how sensitive the current price of a bond is to changes in the key rate - this is important to consider when buying a bond.
If the yield is the same, you need to choose bonds with a shorter duration.
Bond prices and interest rates move in opposite directions (think seesaw): as one side goes up, the other goes down (and vice versa). Bonds with long (long) duration are more sensitive to interest rate fluctuations.
Thus, duration is an indicator of risk .
The main thing you need to understand is: The higher the duration, the higher the risk for the investor!
Duration also allows you to evaluate other financial assets with fixed payments. For example, banks can calculate the duration of loans and loan portfolios. But that is another story.
How changes in interest rates affect bond prices
The dynamics of market prices for bonds largely depends on changes in interest rates. At the same time, there is an inverse relationship: when rates rise, the market price decreases, and when rates fall, it increases.
This dependence is not always equivalent. For example, if rates fall by 5%, the value of the security may rise by the same 5%. If rates rise by 5%, the bond will fall in price by 4%.
The key rate of the Central Bank has a decisive influence on the yield of debt obligations. If the key rate increases, coupon bonds fall in price. When the key rate falls, the market value of such securities increases.
The monetary duration formula (according to Macaulay) does not take into account changes in rates. To calculate the payback period of investments at variable rates, it is better to use the indicators of effective duration and modified duration of bonds.
Duration. What is it and why is it important
When talking about debt instruments, you can often come across a term such as duration. In this review, we will look at what this indicator means and how to apply it in practice.
When purchasing a bond, an investor takes on two key risks: credit - the risk of default by the issuer, and interest rate - the risk of fluctuations in the market value of the security in response to changes in the level of interest rates in the economy.
Example of interest rate risk: There is a fixed coupon bond trading at par 100% with a yield of 8% per year. Due to changes in the market situation, the yield on similar instruments increased to 10%. Accordingly, for our paper to be of interest to investors, it must provide similar returns. But since the coupon was previously fixed at 8%, such a yield can only be achieved by reducing the cost of purchasing the bond. The market price of the paper decreases and becomes less than its face value. This is the interest rate risk of bonds - their price falls when market yields rise and, conversely, rises when they fall.
To measure and compare the interest risks of different debt securities, the duration indicator was introduced.
How to measure the level of interest rate risk
The first key factor that influences interest rate risk is time to maturity.
Example: there are two absolutely identical bonds maturing in 3 years and 5 years. Due to an increase in the key rate by 1%, the yield on such bonds on the market also increased by 1%. Accordingly, to compensate for the difference in yield to maturity, a 3-year bond should trade 1% * 3 years = 3% below its initial cost, a 5-year bond - 1% * 5 years = 5%.
The example is simplified, but clearly shows how interest rate risk relates to maturity. However, in addition to the maturity date, the size of the coupon also matters. All other things being equal, securities with a larger coupon will be more attractive to investors. This means that a bond with a 20% coupon will decrease in price less if rates rise than a bond with a 10% coupon with the same maturity.
In 1938, Frederick Macaulay developed his method of taking coupons into account when assessing interest rate risk. He proposed comparing bonds not by maturity, but by the weighted average period until receipt of coupons and par value.
In the Macaulay formula, each payment on a bond receives its weight depending on the period when it will be received using the discounting method: the earlier the payment arrives, the higher its weight. The amount of weighted payments is divided by the current market price and the desired result is obtained. Macaulay proposed to call the new indicator duration (from the English duration - duration).
where: P is the current price of the bond;
r—yield to maturity/offer;
t is the date of receipt of payment (coupon or face value);
N—bond par value (in money);
C—coupon payment;
n is the number of payments.
Macaulay duration is the basis for calculating other indicators related to bond price volatility. Since it represents a time period, it can be measured in days. This is exactly how it can be seen in the QUIK terminal.
The higher the duration of a bond issue, the more strongly it reacts to changes in the required yield. In other words, the higher the duration, the higher the interest rate risk.
It is worth noting a number of features characteristic of duration:
— All other things being equal, the longer the term to maturity, the higher the duration.
— All other things being equal, the higher the coupon value and the more often it is paid, the lower the duration.
— All other things being equal, the higher the yield to maturity, the lower the duration.
— The Macaulay duration of a zero-coupon bond is equal to the term to maturity.
Application in practice
In practice, modified duration (MD) is usually used, which is calculated based on the Macaulay duration using a simple formula:
Considering that in QUIK the Macaulay duration is measured in days, the resulting value must be divided by another 365. For example, let’s calculate the MD for the OFZ-PD issue 25083 using the indicators from the table in the previous picture. We get 1092 / ((1+ 0.0821)*365) = 2,76.
Modified duration is a dimensionless quantity, and its mathematical meaning is as follows: modified duration is an approximate change in the value of a bond in response to a 1% (100 basis points) change in yield.
Δ P = -MD * Δy,
where ΔP is the change in the value of the bond, Δy is the change in yield.
Using this formula, you can estimate the change in the value of a bond with small changes in yield.
Example: Bond with a par value of 1000 rubles. trading at a price of 101.7% (RUB 1,017), with a yield of 8% and a modified duration of 1.72. If market yields rise from 8% to 10%, then the bond's value will change by approximately -1.72 * (0.1-0.08) = -0.0344 = -3.44%. The paper will trade at a price of 1017 * (1 - 0.0344) = 982.02 rubles. ( 98.2% of face value)
The modified duration of a bond portfolio consisting of several securities is simply calculated as the sum of the products of the duration of each issue and its share:
Example: a portfolio is made up of two securities. The share of the first paper is 30%, its duration is 0.8. The share of the second paper is 70%, duration 1.4. The duration of the entire portfolio will be equal to 0.3*0.8 + 0.7*1.4 = 1,22.
When forming a portfolio, duration is used according to the following strategy:
If interest rates are expected to decline, then the investor should increase the duration of the portfolio in order to extract greater profits due to rising prices.
If interest rates are expected to rise, then it is worth reducing the duration of the portfolio to reduce losses from falling prices.
If you do not have a formed opinion about the future dynamics of interest rates, form a portfolio so that its duration is approximately equal to the period of the intended investment.
An important point: the duration in the QUIK terminal takes into account the duration of bonds with a variable coupon until the date of the nearest put offer. But the call offer is not taken into account in the terminal. The duration to the call offer can be calculated independently using the formula, or viewed on specialized resources such as cbonds.ru and rusbonds.ru.
Convex
For the average private investor, the amount of information provided above is quite sufficient to manage the interest rate risk of a small portfolio using duration. But for more accurate calculations, the importance of which increases with the growth of the amount and timing of investments, it is necessary to become familiar with one more concept.
As stated earlier, modified duration is only a rough estimate and is only suitable for small changes in yield. The thing is that the dependence of the price of a bond on its yield is not linear, but is a curve:
Thus, the greater the change in the interest rate, the more the real change in value will deviate from the calculated one. The range of rates within which the error can be considered insignificant depends on the parameters of a particular bond and the amount of funds that are planned to be invested in it.
The second important point is the asymmetry of the Price/Yield chart. If the interest rate decreases by 1%, the price will increase more than it will decrease with a similar rate increase of 1%.
In order to reduce the calculation error, another parameter is used that characterizes the convexity of the Price/Yield curve. It is called convexity, or the term convection is also used.
The mathematical meaning of convexity is beyond the scope of this article, but for practical use it is, in general, of no use to an ordinary private investor. The value of convexity can be found on the same specialized resources like rusbonds.ru or cbonds.ru. Convexity (Vpcl) is included in the calculations as follows:
The first term in this formula, which you have already seen earlier, is called the percentage change in price due to duration. The second term is, respectively, the percentage change in price due to convexity.
The second term corrects the value calculated by duration and introduces asymmetry into it. Positive convexity, characteristic of ordinary bonds, adjusts the result towards higher prices and is a positive moment for the investor.
Using duration and convexity together provides a more accurate measure of the change in bond yields in response to shifts in interest rates.
All other things being equal, greater convexity is more profitable for the investor.
The graph clearly shows that with the same duration, the more convex bond B turns out to be more profitable for the investor if interest rates change significantly. When rates fall, it grows in price faster, and when they rise, it loses its value more slowly.
If investors in the market expect high interest rate volatility, market participants may prefer those with higher convexity among securities with the same duration. This will show up as lower yields on those bonds.
Conversely, when rate volatility is expected to be low, investors are reluctant to sacrifice yield for convexity and will move capital into higher-yielding securities. A private investor can use this pattern as an indicator of sentiment in the debt market.
The convexity of the entire bond portfolio is measured similarly to the duration of the portfolio: the convexity of each security is multiplied by its weight in the portfolio and the resulting values are added.
Features of using duration
A natural question may arise: why not simply use the function Price = f (yield) instead of duration and convexity. However, such calculations turn out to be too cumbersome even when using computer technology. Very often, duration and convexity make it possible to obtain a good approximation of the desired value with an acceptable level of error.
The duration and convexity figures shown are valid only for ordinary bonds without embedded options. If changes in yields lead to changes in the bond's expected cash flows, then duration and convexity measures are applicable only in some specific cases.
The concept of duration and assessment of interest rate risk of debt securities in general is not limited to the indicators presented in this review. However, for the average private investor, these concepts are enough to intelligently formulate a bond portfolio taking into account interest rate risk. If you want to delve even deeper into bond portfolio management techniques, we recommend that you read specialized literature, for example, Frank Fabozzi “Bond Market. Analysis and Strategies".
Open an account
BCS Broker
Example of determining duration
Let's consider an example in which we calculate the duration for a “mixed” portfolio, including coupon and zero-coupon OFZs, as well as corporate securities.
So, the investor's portfolio looks like this:
| Name of the security | Face value, $ | Market price, $ | Maturity period, years | Coupon, % | Number of payments per year | Duration, years | Portfolio share, % |
| OFZ | |||||||
| 1 | 12,5 | 12,6 | 6 | 7,75 | 2 | 0,07 | 5 |
| 2 | 12,5 | 13 | 7 | 11 | 3 | 0,07 | 5 |
| 3 | 12,5 | 11 | 2 | 2 | 10 | ||
| 4 | 12,5 | 14 | 9 | 10 | 1 | 0,16 | 10 |
| 5 | 12,5 | 17 | 10 | 9 | 3 | 0,04 | 10 |
| Corporate | |||||||
| VEB | 12,5 | 12,5 | 5 | 11,6 | 1 | 0,30 | 10 |
| Gazprom | 12,5 | 10,6 | 4 | 7,7 | 2 | 0,09 | 10 |
| Rolf | 12,5 | 11,5 | 2 | 9 | 4 | 0,09 | 10 |
| RESO-Leasing | 12,5 | 12,3 | 2 | 9,7 | 2 | 0,18 | 10 |
| Garant-Invest | 12,5 | 11,2 | 2 | 13,5 | 4 | 0,12 | 10 |
| Tinkoff | 12,5 | 12,9 | 2 | 7,3 | 2 | 0,16 | 10 |
We see that all securities, with the exception of zero-coupon securities, will pay off in the first year after acquisition.
Therefore, the portfolio consists of low-risk bonds. Using the above formula, we calculate the duration of the portfolio and get a value of 0.14.
Macaulay duration: calculation formula
The most well-known method for calculating duration is the Macaulay formula. Macaulay duration is the weighted average time until coupons and par are received. Macaulay duration is measured in years.
In the Macaulay formula, each payment on a bond receives its weight depending on the period when it will be received using the discounting method: the earlier the payment arrives, the higher its weight. The amount of weighted payments is divided by the current market price and the desired result is obtained.
The formula is quite complex and confusing, so ordinary investors rarely resort to independent calculations using it, preferring to use special services with ready-made values for each type of bond. This value can be seen in the terminal in QUIK.
Simplified explanation of the formula:
In the numerator: Amount of (receipt on the bond * time of receipt) Denominator: Bond price + cash income
Bond proceeds are all future payments: coupons and redemptions. Since these are future payments at different times, we need to somehow bring them to today. From a mathematical point of view, these payments should be exempt from profitability, that is, discounted. This is done because 1000 rubles now is NOT EQUAL to this amount in 1 year, in 2 years, etc. Discounting is the reverse process of interest.
It is more important to simply understand that the duration of bonds depends on the price and the remaining period until maturity, while:
- At a constant price, if the time to maturity decreases, the duration also decreases.
- With a constant term, if the price of a bond rises, then the duration also decreases; if the price decreases, it increases.
Thus, the duration of bonds is constantly changing, it is recalculated every day and will be different every day.
How to use duration in practice
So, let's summarize the concept of duration in simple words, so that it is clear even for children: we lend money at interest and we need to know how soon we can return our funds so as not to remain at a loss. It is clear that when lending money to a person with or without interest, we always accept the risk of non-repayment or delay.
In the case of securities, such a risk also exists, but debt securities have their own advantage: they can be sold before maturity at the current market price.
If you buy bonds and hold them to maturity, you don't really need duration. But if you are a trader, you need it. Of course, you don’t need to independently calculate the payback period of paper using a complex formula, because it will take a lot of time and there is a high probability of error. You can use special online services and trading terminals.
How to find out duration
You don't need to calculate anything yourself. You can usually view the duration value in services with a bond yield calculator. This will help you make an informed decision regarding investments in certain bonds.
You can find a bond yield calculator here:
- Bond calculator on rusbonds.
- Calculator on the Moscow Exchange website.
- At smart-lab.
- cbonds.ru (paid tools).
The duration value is also available in the QUIK trading terminal.
Let's look at the first example.
How to use the calculator:
- by going to the website page, from the “Name” drop-down list, you need to select the desired bond that is suitable in terms of yield;
- in the field “Calculation by price” - “Net price”, enter the market price at the moment, which is now;
- Click the “Calculate” button.
You can also see the duration value on the rusbonds website on the bonds pages in the “Yield” tab.
Relationship between convexity and duration
If an investor graphically represents the yield from a bond, he will not get a straight line, but a convex curve, the bend or “convexity” of which depends on the yield of the security.
The concept of “convexity” is a financial term that characterizes the dependence of the value of a bond on its yield. “Convexity” is directly related to duration and reflects the property of its change - the greater the rate of change, the more the duration changes.
The convexity graph looks like this:
For an investor, the meaning of "convexity" indicates that the more convex a particular bond is, the faster the yield rises, but also the lower the value of the bond becomes.
Bond duration: calculation, formula
The duration value can be used to characterize many investment instruments, but most often it is used to take into account the risks when using securities with a specified maturity.
The most common use of the duration indicator is to calculate the duration of a bond. As mentioned above, the duration of a bond is identical to the general concept of duration, which is a certain number of years required to repay the full cost of the bond.
A bond is an issue-grade debt security and its market value may change during the period of its full repayment.
Duration allows an investor to fully assess the financial attractiveness of bonds on the securities market, taking into account several important indicators at once - the period for which the bond is issued, the interest rate (coupon), and the par value of the security. The calculated bond duration indicator will help investors decide on the allocation of a portfolio of securities with the greatest profit.
The duration of a security can be calculated in several ways:
Duration formula - how to calculate the value
Duration depends on three components: price, interest rate and maturity
De = [Pi- + Pi+ ] / [Pr &timex; (i+ — i—) ]
Where:
- De – the value of the effective duration of the bond
- Pi- – market price when the rate decreases
- Pi+ – market price when the rate increases
- Pr – nominal price of the security
- i+ – increased starting rate
- i— – reduced starting rate
There is no need to calculate the bond duration yourself using the formula. It has already been calculated automatically. The data can be viewed in the QUIK trading terminal or in open sources on bonds: https://www.rusbonds.ru (for example).
The difficulty with the formula is that current money does not equal tomorrow's money. Therefore, for the accuracy of calculations, they should be discounted.
There is also another duration formula that also takes into account the discount rate:
D = [ ( [∑ t × C] / (1+i)t) + ( / (1+i)n)] / p
Where:
- n – number of payments
- t – period required for full repayment
- M – repayment of the nominal price of the bond
- C – cash receipts of interest income
- i – discount rate
- p – market price of the bond
Duration Macaulay
Frederick Macaulay derived a formula for calculating duration back in the 30s of the last century, but its practical use in Russia began only in 1993.
The formula looks like this:
- where D is duration,
- n – number of payments,
- t – time required for full repayment,
- M – redemption of the nominal value of the security,
- C – cash flow of interest income,
- i – discount rate,
- p – market value of the security
For example, an investor has two bonds with a par value of 5,000 rubles each, one of them with a zero coupon (zero coupon) and a maturity of 3 years, the other with a coupon equal to 5%, which is paid annually, also with a maturity of 3 years.
In the first case, the duration will be equal to the maturity of the bond, namely 3 years, since the cash flow of interest income is 0.
In the second case, the calculation can be made as follows:
The duration of a bond with a 5% coupon will be 2.86 years.
Modified duration
If the interest rate of return changes in any time period until the full repayment of the nominal value, then it is necessary to use the modified duration formula for calculation:
Dm= D/(1+ Cm/n)
- where Dm is the modified duration,
- Cm – yield to maturity,
- n – number of coupon payments per year
Applying the previous calculation, we calculate Dm= 2.86/((1+0.05/1))=2.86/1.05=2.72
Thus, as the coupon income increases, the duration decreases.
However, the modified duration is applicable only if the income cash flows do not change with changes in the interest rate, which is most often impossible in practical applications. For the calculation, a more sensitive tool is needed to fluctuations in the interest rate and, accordingly, profitability, which is the effective duration.
Effective Duration
When calculating the effective duration of a bond, fluctuations in interest rates, both downward and upward, are taken into account. The formula for calculation is as follows:
- Where De is the effective duration,
- Pi- is the value of the bond when the interest rate decreases,
- Pi+ is the value of the bond when the interest rate increases,
- Po is the initial value of the bond,
- i+ - increased initial interest rate,
- i- — reduced initial interest rate.
The calculation of effective duration is applicable using a binomial interest tree to calculate the value of a bond, taking into account fluctuations in interest rates.
Duration calculation example
Let's model the calculation schemes for DO using two types of similar instruments. To do this, let’s compare OFZs with a nominal value of 1 thousand rubles. The redemption period is 12 months. Profitability – 10%. The amount of payments for the year is 100 rubles. Only the frequency of cash receipts differs:
- Coupons are issued 2 times a year. The cost of the coupon is 50 rubles.
- Payments are made quarterly (4 times a year). Coupon price – 25 rubles.
The table shows the main parameters of the instruments:
| Index | №1 | №2 |
| Denomination, rub. | 1 000 | 1 000 |
| Coupon size, in rubles. | 50 | 25 |
| Number of payments | 2 | 4 |
| Payment schedule | — | — |
| 01.04.2020 | — | 25 |
| 01.07.2020 | 50 | 25 |
| 01.10.2020 | 25 | |
| 01.01.2021 | 50 | 25 |
| Redemption amount, rub. | 1 100 | 1 100 |
Calculation formula No. 1:
The total number of days of duration is less than 1 year. Calculations were made based on annual figures, but without discounting. This simplified the task and did not affect the final result.
Calculation formula No. 2:
The value in the second example is slightly smaller. The reason is faster return of coupon payments. The cost of the financial instrument will pay off faster.
It is more profitable for an investor to choose OFZ with a lower DO. This will reduce risks and ensure active capital movement. Therefore, the investor will get more profit by reinvesting the funds.
Increased risk is also inherent in zero-coupon bonds. There are no interim payments for them. Payment of income is made in a lump sum.
For the issue of bonds with a cash flow determined before the redemption date, the duration is calculated to maturity. For issues of securities with unexecuted offers and partially determined cash flow, the indicator is calculated against the offer.
Perpetual bonds
A perpetual bond is suitable for investors who want to receive stable income for a long time. The paper does not provide for the redemption of the face value. Its owner is entitled only to coupon profit. But the terms of the issue may say that the subsidiary has a certain period. For example, forced repayment (call option) of OFZ (KO) is made after 10 years.
The first placement of perpetual bonds on the Moscow Exchange was carried out by VTB Bank in 2012. Later, Gazprombank and Promsvyazbank entered the market. In 2016, Alfa Bank and TKS Bank (Tinkoff) began using financial instruments.
Perpetual bonds were issued in the form of Eurobonds in foreign currency. The minimum lot price started at $100,000. Perpetual bond coupons could be fixed or floating. VTB Bank and Gazprombank tied coupon payments to 5 and 10-year US government bonds (+ 7.1 and 8.1%, respectively). Call options were scheduled for 2022 and 2022.
Only Rosselkhozbank managed to issue ruble bonds. From 2018, not only banks, but also other financial companies can enter the market.
In 2022, JSC Russian Railways placed Eurobonds series 001B-04 in the amount of 80 billion rubles. The coupon rate is 7.25% per annum. The securities have call options every five years. Several organizations acted as organizers: VTB Capital, MKB, Sberbank CIB, Promsvyazbank, BC Region and Rosselkhozbank.
A perpetual bond is considered a fairly profitable investment instrument. However, paper is not immune to all risks. When a company (issuer) goes bankrupt, it does not provide noticeable benefits to its owner.
Bonds with an offer
It is possible to make a correct calculation of DO with accurately formed coupon payments. Payment amount and coupon rate may vary. However, these data must be known subsequently.
Offer – a proposal to conclude an agreement addressed to a narrow or unlimited circle of persons. The contract is considered concluded as soon as the recipient agrees to its terms.
Of course, sometimes there are bonds for which there is no data on future payments. For example, securities with a floating coupon or KO with an irrevocable offer.
Calculation of DO with a floating coupon will not be accurate. Consequently, it will not provide the investor with useful information. For corporate securities, the duration must be calculated at the time of the offer, equating it to the redemption date. The offer can be considered as a possibility of premature redemption of the KO. Calculation formula:
Where:
- numerator – the difference between the value of a government bond against the backdrop of a rate decrease and its price during a rate increase;
- the denominator is the base value of the paper multiplied by the difference between the rates.
Calculations show that the indicator is significantly shorter than the redemption time. For example, for the FGC UES B4 bond there are 12,243 days left until the repurchase, and 1,421 days until the repurchase.
The reason is that duration is calculated based on the time of the offer. DO cannot be longer than the period before the paper is redeemed. Maximum – the indicator will be equal to the redemption time. For example, if the coupon is paid at a time or we are talking about OFZ (KO) of a zero-coupon type.
Definition of the concept
In simple words, the duration of a bond (DO) is the number of calendar days or years after which the trader fully reimburses the expenses incurred when purchasing a security . The lower the indicator, the shorter the period and, accordingly, the lower the investment risk.
The duration value depends on several factors - the type of security, coupon percentage, and frequency of payments.
Let's look at a few examples:
- Bond with a 25% coupon. The term of full repayment of the paper is 5 years, the nominal price is 50 thousand rubles, the investor receives interest once a quarter. Accordingly, 12.5 thousand rubles are received once every 3 months and the trader returns the invested 50 thousand in a year. In this case, the duration is 365 days.
- A bond without a coupon with a maturity of 5 years. In this option, the investor receives the invested funds only after 5 full years, the duration will be 1825 days.
From the two examples, it is clear that a security without a coupon will be riskier, since it will take longer to fully recoup the money spent. The higher the coupon percentage, the lower the duration. If the investor chooses the option without a coupon, then the duration will fully correspond to the repayment period.
For a simpler understanding, we can draw an analogy with lending. If the borrower makes monthly interest payments, the bank bears less risk by receiving money from the first month. In the case when the loan and interest are repaid on the last day of the contract, the risk is much higher, and the period for repayment of the investment is longer.
Important! The duration of coupon bonds is always lower than that of zero-coupon securities.
Read more: about coupon bonds.