What is BFT? The task of the Byzantine generals. Examples [2019]

The Byzantine general problem (BFT) is one of the fundamental properties of reliable blockchain rules or protocols.

Blockchain allows computers and people to agree on things without having to trust each other. This network of people and computers simply has to trust that the rules they all follow are reliable.

The Byzantine general problem (BFT) is one of the fundamental properties of creating reliable rules or blockchain protocols.

But before we can understand what Byzantine fault tolerance is, we need to take a step back and understand what nodes and consensus mean.

What are peers and nodes?

Most blockchains or cryptocurrencies operate as networks, where all computers on the network have equal access and rights, and communicate directly with each other. Each individual computer on this network is known as a host or node.

In a truly decentralized system, no one node has more power or authority than the next. This means that there are no managers, coordinators, or directors to enforce rules, determine what is true, or punish inappropriate behavior.

Instead, the system relies on the fact that all nodes must follow the same rules or protocol to reach an agreement.

Inclusive and exclusive blockchains

An exclusive blockchain is one where permission is required to participate in the network, whereas an inclusive blockchain network can be joined by anyone. Also, participants in an exclusive blockchain can enjoy full or selective privileges.

Private and public blockchains

A private blockchain is one that resides on a private network. (For example, you run a private version of Ethereum on your computer to study smart contracts.) It is isolated, so others cannot see it and cannot join your network. To have access to a private blockchain, you must be invited and approved by the network administrator or subject to certain rules and restrictions.

The public blockchain is completely open and anyone can join the network and contribute. Examples of public exclusive blockchains are Ripple and EOS, where ordinary participants have fewer powers than privileged ones, such as unique nodes (in Ripple) or block creators (in EOS).

Public inclusive blockchains include Bitcoin, Ethereum and the like.

Examples of private exclusive blockchains are when you run your own version of Hyperledger or Ethereum on your computer, or a private blockchain within a company.

Blockchain consortiums

The last type is blockchain consortia, where a group of participants (most likely multinational corporations) form a network (you can think of it as a kind of “intranet”) and only they can join and use it. Examples of blockchain consortiums are Hyperledger from the Linux Foundation and Quorum from JP Morgan.

Source: crypto.com

What is consensus?

Consensus simply means general agreement. In a decentralized system where there is no power, achieving consensus is one of the most important and difficult tasks.

Find out about all types of consensus in blockchain in our article!

For a system or network to function properly, a majority of nodes must agree on what is true, reaching consensus at regular intervals.

The problem is that some nodes will inevitably fail, misbehave, or simply disagree with the consensus of other nodes, so the system must be designed to deal with this problem.

Proof of the stability of cryptocurrency systems

Another property of Bitcoin was discovered by the famous American scientist Leslie Lamport. He proved that agreement at the headquarters of N generals can be achieved only if the number of defectors does not exceed N/2 minus one general. This rule, which works when generating bitcoins, is called the “51 percent rule.” To put it simply, if the powers of traitors exceed the powers of honest generals, then the latter will not be able to build a correct system of vectors due to a lack of correct information. In the case of bitcoins, this will allow “defectors” to selectively confirm other people’s blocks, and therefore control the process of mining cryptocurrency.

New Bitcoins are mined correctly as long as the blockchain community is dominated by bona fide participants

Why then, after eight years of existence, has no one yet managed to hack the Bitcoin network? Because today such an attack would require power many times greater than the power of the world’s computers combined. And, as in the case of the general staff, in which there are more traitors than loyal generals, the reasons for such a situation will lie in a completely different plane than the exchange of information.

The solution to the generals problem based on the blockchain platform is also applicable to other areas where distributed network users lack trust: domain name systems, referendums, elections, etc., and the number of generals in the problem condition can be infinite.

2shares
0
0
2

What is the task of the Byzantine generals?

The Byzantine General Facility (BFT) system can continue to work correctly as long as two-thirds of the network agrees or reaches consensus. BFT is a property or characteristic of a system that can withstand up to one third of nodes that fail or act maliciously.

All decentralized blockchains operate under agreed upon protocols or rules that all nodes on the blockchain must follow in order to participate. Consensus protocols such as Proof-of-Work and Proof-of-Stake are BFT and are thus able to withstand one-third of non-consensus nodes.

Links[edit]

Kirrmann, Hubert (b). "Fault Tolerant Computing in Industrial Automation" (PDF). Switzerland: ABB Research Center. item 94. Archived from the original (PDF) on March 26, 2014. Retrieved March 2, 2015.
Lamport, L.; Shostak, R.; Pease, M. (1982). "The Problem of the Byzantine Generals" (PDF). ACM Transactions on Programming Languages and Systems
.
4
(3): 382–401. CiteSeerX 10.1.1.64.2312. DOI: 10.1145/357172.357176. Archived from the original on June 13, 2022 (PDF).
^ abc Driscoll, K.; Hall, B.; Paulitsch, M.; Zumsteg, P.; Sivencrona, H. (2004). "Real Byzantine generals." 23rd Digital Avionics Systems Conference (IEEE Cat. No. 04CH37576)
. P. 6.D.4–61–11. DOI: 10.1109/DASC.2004.1390734. ISBN 978-0-7803-8539-9. S2CID 15549497.
^ abc Driscoll, Kevin; Hall, Brendan; Sivenkrona, Hakan; Zumsteg, Phil (2003). "Byzantine fault tolerance, from theory to reality." Computer Security, Reliability and Security
.
Lecture notes on computer science. 2788
. pp. 235–248. DOI: 10.1007/978-3-540-39878-3_19. ISBN 978-3-540-20126-7. ISSN 0302-9743. S2CID 12690337.
Avizienis, A.; Laprie, J.-C.; Randall, Brian; Landwehr, K. (2004). "Basic concepts and taxonomy of reliable and secure computing." IEEE Transactions on Dependable and Secure Computing
.
1
(1): 11–33. DOI: 10.1109/TDSC.2004.2. hdl: 1903/6459. ISSN 1545-5971. S2CID 215753451.
"Reliable Computing and Fault Tolerance". Archived from the original on April 2, 2015. Retrieved March 2, 2015.
Generalized Communication and SecurityModelsin Byzantine Agreement, Matthias Fitzi https://www.crypto.ethz.ch/publications/files/Fitzi03.pdf
^ a b "SIFT: design and analysis of a fault-tolerant computer for aircraft control." Reliability of microelectronics
.
19
(3):190. 1979. DOI: 10.1016/0026-2714(79)90211-7. ISSN 0026-2714.
Pease, Marshall; Szostak, Robert; Lamport, Leslie (April 1980). “Reaching an agreement when there are deficiencies.” Journal of the Association for Computing Machinery
.
27
(2):228–234. CiteSeerX 10.1.1.68.4044 . DOI: 10.1145/322186.322188. S2CID 6429068.
Lamport, Leslie (2016-12-19). "The Problem of the Byzantine Generals". ACM Transactions on Programming Languages and Systems
. SRI International. Retrieved March 18, 2022.
^ a b c Lamport, L.; Shostak, R.; Pease, M. (1982). "The Problem of the Byzantine Generals" (PDF). ACM Transactions on Programming Languages and Systems
.
4
(3):387–389. CiteSeerX 10.1.1.64.2312. DOI: 10.1145/357172.357176. Archived from the original (PDF) on February 7, 2022.
Driscoll, Kevin (2012-12-11). "Real System Failures". DASHlink
. NASA. Archived from the original on April 2, 2015. Retrieved March 2, 2015.
Walter, C.; Ellis, P.; LaValley, B. (2005). “Reliable Platform-Service: A Resilient Property-Based Service Architecture.” Ninth IEEE International Symposium on High Assurance Systems Engineering (HASE'05)
. pp. 34–43. DOI: 10.1109/HASE.2005.23. ISBN 978-0-7695-2377-4. S2CID 21468069.
Feldman, P.; Micali, S. (1997). "An optimal probabilistic protocol for synchronous Byzantine agreement" (PDF). SIAM J. Comput
.
26
(4):873–933. DOI: 10.1137/s0097539790187084. Archived (PDF) from the original on March 5, 2016. Retrieved June 14, 2012.
Paulitsch, M.; Morris, J.; Hall, B.; Driscoll, K.; Latronico, E.; Koopman, P. (2005). "Covering and exploiting cyclic redundancy codes in ultra-reliable systems." 2005 International Conference on Dependable Systems and Networks (DSN'05)
. pp. 346–355. DOI: 10.1109/DSN.2005.31. ISBN 978-0-7695-2282-1. S2CID 14096385.
Hopkins, Albert L.; Lala, Jaynarayan H.; Smith, T. Basil (1987). "The Evolution of Fault-Tolerant Computing at the Charles Stark Draper Laboratory, 1955–85." The Evolution of Fault-Tolerant Computing
.
Reliable computing and fault-tolerant systems. 1
. pp. 121–140. DOI: 10.1007/978-3-7091-8871-2_6. ISBN 978-3-7091-8873-6. ISSN 0932-5581.
Driscoll, Kevin; Papadopoulos, Gregory; Nelson, Scott; Hartmann, Gary; Ramohalli, Gotham (1984), Multi-microprocessor flight control system
(technical report), Wright-Patterson AFB, OH 45433, USA: AFWAL/FIGL USAF Systems Command, AFWAL-TR-84-3076CS1 maint: location (link)
Castro, M.; Liskov, B. (2002). "Practical Byzantine Fault Tolerance and Proactive Recovery." ACM Transactions on Computer Systems
.
Association for Computing Machinery. 20
(4): 398–461. CiteSeerX 10.1.1.127.6130. DOI: 10.1145/571637.571640. S2CID 18793794.
↑
Abd-El-Malek, M.;
Ganger, G.; Good song.; Reiter, M.; Wiley, J. (2005). "Fault-tolerant Byzantine fault-tolerant services." ACM SIGOPS Operating Systems Survey
.
Association for Computing Machinery. 39
(5): 59. DOI: 10.1145/1095809.1095817.
Cowling, James; Myers, Daniel; Liskov, Varvara; Rodriguez, Rodrigo; Srira, Lyuba (2006). HQ Replication: A Hybrid Quorum Protocol for Byzantine Fault Tolerance. Proceedings of the 7th USENIX Symposium on Operating Systems Design and Implementation. pp. 177–190. ISBN 1-931971-47-1.
Kotla, Ramakrishna; Alvisi, Lorenzo; Dahlin, Mike; Clement, Allen; Wong, Edmund (December 2009). "Zyzyva: Speculative Byzantine Fault Tolerance". ACM Transactions on Computer Systems
.
Association for Computing Machinery. 27
(4): 1–39. DOI: 10.1145/1658357.1658358.
Guerraoui, Rachid; Knezevic, Nikola; Vukolić, Marko; Kema, Vivien (2010). The next 700 BFT protocols. Proceedings of the 5th European Conference on Computer Systems. EuroSys. Archived from the original on October 2, 2011. Retrieved October 4, 2011.
Clement, A.; Wong, E.; Alvisi, L.; Dahlin, M.; Marchetti, M. (22–24 April 2009). Making Byzantine Fault Tolerant Systems Resilient to Byzantine Failures (PDF). Symposium on Design and Implementation of Networked Systems. USENIX. Archived (PDF) from the original on December 25, 2010. Retrieved February 17, 2010.
Aublin, P.-L.; Ben Mokhtar, S.; Quéma, V. (July 8–11, 2013). RBFT: Redundant Byzantine Fault Tolerance. 33rd IEEE International Conference on Distributed Computing Systems. International Conference on Distributed Computing Systems. Archived from the original on August 5, 2013.
Bahsoun, J.P.; Guerraoui, R.; Shocker, A. (05/01/2015). "How to Make BFT Protocols Truly Adaptive". Parallel and Distributed Processing Symposium (IPDPS), 2015 IEEE International
: 904–913. DOI: 10.1109/IPDPS.2015.21. ISBN 978-1-4799-8649-1. S2CID 16310807.
↑
Chun, Byung-Gon;
Maniatis, Petros; Schenker, Scott; Kubiatowicz, John (01/01/2007). “Verified Memory, Designed for Addition Only: Making Opponents Stick to Their Word.” Proceedings of the Twenty-First ACM SIGOPS Symposium on Operating Systems Principles
. SOSP '07. New York, NY, USA: ACM: 189–204. DOI: 10.1145/1294261.1294280. ISBN 9781595935915. S2CID 6685352.
Veronese, G.S.; Correia, M.; Bessani, AN; Lung, LC; Verissimo, P. (2013, January 1). "Efficient Byzantine fault tolerance". IEEE Transactions on Computers
.
62
(1): 16–30. CiteSeerX 10.1.1.408.9972. DOI: 10.1109/TC.2011.221. ISSN 0018-9340. S2CID 8157723.
Buchman, E.; Kwon, J.; Milosevic, Z. (2018). "Latest BFT Consensus Rumors." arXiv: 1807.04938 [cs.DC].
"Bitcoin - Open Source P2P Money". bitcoin.org
. Retrieved August 18, 2022.
M., Paulich; Driscoll, K. (January 9, 2015). "Chapter 48: SAFEbus". In Zurawski, Richard (ed.). Handbook of Industrial Communications Technologies, Second Edition
. CRC Press. pp. 48–1–48–26. ISBN 978-1-4822-0733-0.
Thomas A. Henzinger; Christophe M. Kirsch (September 26, 2001). Embedded Software: First International Workshop, EMSOFT 2001, Tahoe City, California, USA, October 8-10, 2001. Proceedings (PDF). Springer Science & Business Media. P. 307–. ISBN 978-3-540-42673-8. Archived (PDF) from the original on September 22, 2015. Retrieved March 5, 2015.
Ye, Y. C. (2001). "Safety-critical avionics for the 777's primary flight control system." 20th DASC. 20th Digital Avionics Systems Conference (Cat. No. 01CH37219)
.
1
. pp. 1C2/1–1C2/11. DOI: 10.1109/DASC.2001.963311. ISBN 978-0-7803-7034-0. S2CID 61489128.
"ELC: SpaceX Lessons Learned [LWN.net]". Archived from the original on August 5, 2016. Retrieved July 21, 2016.
Nanya, T.; Goosen, H. A. (1989). "Byzantine Hardware Fault Model". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems
.
8
(11): 1226–1231. DOI: 10.1109/43.41508. ISSN 0278-0070.
Martins, Rolando; Gandhi, Rajiv; Narasimhan, Priya; Pertet, Soila; Casimiro, Antonio; Kreutz, Diego; Verissimo, Paulo (2013). "Experience of fault injection in the Byzantine fault-tolerant protocol." Middleware 2013
.
Lecture notes on computer science. 8275
. pp. 41–61. DOI: 10.1007/978-3-642-45065-5_3. ISBN 978-3-642-45064-8. ISSN 0302-9743.
US Patent 7475318, Kevin R. Driscoll, "Test Method for Sensitive Input Range of Byzantine Filters", issued 2009-01-06, assigned to Honeywell International Inc.
"Google Code Repository for the UpRight Replication Library". Archived from the original on 2016-04-15.
"BFT-SMaRt Replication Library Repository".
"Github repository for the Archistar project". 2019-05-28. Archived from the original on 2015-02-04.
"Github repository for the Archistar project". 2019-04-28. Archived from the original on 2017-06-13.
"Askemos Home Page". Archived from the original on 2016-05-03.

BFT problems

The concept of BFT comes from the Byzantine General's Problem, which is a logical thought experiment in which there are several generals who must attack a city.

All generals are in different places and can only communicate using messenger, one message at a time.
They all must coordinate the same action to successfully attack or retreat.
If they all attack, they'll be fine. If they all back down, they'll be fine.
The problem comes when some generals attack and others retreat, in which case it will be a bad outcome for everyone.
The point is that some generals are disloyal and will try to confuse other generals.

essence of the problem

The problem that needs to be solved is this: how will all the generals agree to the same action even in the face of betrayal and deceit?

Options for solving the problem

Let's assume that one of the four generals turned out to be a traitor (N = 4, M = 1). Consequently, three loyal military leaders will send correct information about the number of their legionnaires, and in the messages of a traitor the numbers can be anything. Let's say the first general reported that his legion has 1 thousand soldiers, the second - 2 thousand, and the fourth - 4 thousand. The third general (defector) indicated to the others randomly selected numbers x, y, z. From the received data, each military leader forms his own vector:

1st vector - 1,2,x,4;
2nd vector - 1,2,y,4;
3rd vector - 1,2,3,4;
4th vector - 1,2,z,4.

Next, the generals transmit the vectors to each other, while the traitor repeatedly distorts the information. As a result, everyone receives four vectors from which the kernel is formed:

Composing vectors when exchanging information between blockchain participants

The generals then determine the number of warriors in each legion. To calculate the first legion, three numbers are taken: the number of this legion, known from the reports of all generals with the exception of the commander of the first legion itself. If one of the 3 numbers is repeated twice or thrice, it is placed in the final vector. If there are no matches, the value of the resulting vector is defined as “unknown”.

As a result, each loyal general receives his own vector N, in which the first element is equal to the actual number of troops of the first legion (if its commander is not a traitor) or contains false data (if its general works for the enemy). In this case, the vectors of all loyal generals should be identical.

The result looks like this: ( 1,2,f (x,y,z), 4 ) where f (x,y,z) is the value that appears at least twice among the numbers x,y,z or “unknown” in case if all 3 numbers are different. Since x,y,z and the function f (x,y,z) coincided for all the faithful generals, therefore, agreement has been reached and the enemy will be defeated.

What's so special about this system?

The BFT consensus protocol can still coordinate and reach consensus despite some amount of disagreement between nodes.

This is vital for decentralized blockchains such as Ethereum or Bitcoin.

One of Satoshi Nakamoto's important innovations when he/she/they created Bitcoin was to solve the Byzantine General's problem by applying Proof-of-Work to the Bitcoin network. With its BFT property, the Bitcoin network is protected by up to a third of malicious nodes.

Systems requiring BFT are also used in non-blockchain industries such as aviation, space and nuclear power.

All of these industries place a premium on safety and also work with large numbers of interconnected sensors or computers that act as nodes.

These nodes must communicate with each other reliably, and BFT comes into play when a portion of these nodes become faulty, but the system can still continue to function as intended.

Examples[edit]

Several examples of Byzantine failures are given in two equivalent journal articles. [3] [4] These and other examples are described on the NASA DASHlink web pages. [12] These web pages also describe some of the phenomena that can cause Byzantine errors.

Byzantine errors were observed infrequently and irregularly during endurance testing of newly built Virginia-class submarines, at least until 2005 (when problems were publicly reported). [13]

Mistrust in the blockchain

Since there is no server in the blockchain, users have to add and verify information themselves. Moreover, each participant can pursue their personal interests to the detriment of the security of the blockchain. This raises the problem of participants’ distrust of each other. To solve it, mathematical algorithms are used, which will be discussed further.

Imagine that you have assets in your wallet, but another blockchain user thinks that you don’t. Without outside interference, it is difficult to decide which of the two is right. It is necessary to select among the users those who will check transactions and add only the correct ones. Such users are called miners.

Miners are blockchain participants who create new blocks and verify transactions.

To organize the proper work of miners, it is necessary to agree on who they will be and how they will do their work. This is not an easy task, because you need to come up with rules that will be more profitable for miners to follow than to break. This is a classic example of a game theory problem: how to choose a strategy that will be equally beneficial for participants with different interests.

This problem was formulated and solved by mathematicians back in the last century. Now this solution provides security both in the blockchain and in other complex technologies. To understand how miners manage not to violate each other’s interests, let’s look at this problem in more detail.

Considerations

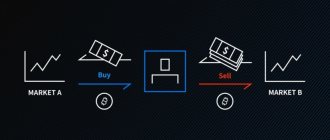
The problem for the two Byzantine generals is the same as when money is transferred without a reliable intermediary. [ 1 ] Bitcoin offered the first practical solution to this problem.
In the real world, lines fail unintentionally. Error detection codes can be used to detect errors. In a verbal communications scenario, a failed line may be considered a traitorous node. If signed messages are used, line failure will be irrefutably detected.
To recognize the sender of a message using verbal messages, you must have fixed lines, not communications networks. In signed messages there are no problems with recognizing the sender.
The absence of messages is usually determined by timeout (time restrictions).
In the real world, it is never guaranteed that a random error cannot forge a signature. However, this has a very low probability with proper signature methods.
Preventing intentional fraud becomes a cryptographic issue. Therefore, it is important to choose secure signature algorithms.
This should be detected if a message is sent twice by checking its signature. Thus, a signature cannot be generated if the process has already seen the same signature at another time.

Russian Blogs

If you are a general of some ancient country, in your country there are 9 generals besides you, each of whom leads an army, a total of 10 armies, and these 10 armies are scattered throughout the region. Your country wants to attack a powerful enemy country, and this enemy country also has a certain strength, enough to withstand the simultaneous attacks of your 5 armies. Therefore, your 10 armies must reach a consensus, at least a majority of the armies must reach an agreement before the enemy is smoothly destroyed.

However, due to special geographical reasons, your 10 armies cannot gather together for one point of attack and must simultaneously encircle and attack the enemy country in a separate state. If it is one army attacking alone, there is no chance of victory unless at least 6 armies are sent simultaneously to attack the enemy country. You are dispersed throughout the enemy country, relying on signal troops to communicate with each other to agree on the intentions and timing of the attack.

The problem that's troubling your 10 generals currently is that you don't have a central leader. 10 generals are equal, and there may be traitors among you. Traitors may change their intentions or attack timing without permission, or even go through false attacks. News, in this state, can you 10 generals find a distributed cooperation method that allows you to negotiate remotely and accurately to win the battle?

This is the famous “problem of the Byzantine generals.”

The challenge of the Byzantine Generals is to solve the problem of the decentralized consensus mechanism, and this consensus problem is also what the Bitcoin blockchain network needs to solve.

Since Byzantine generals are dispersed and have no central governing body, they must agree in advance on the place and time of attack and reach consensus when attacking the enemy. Then, within a limited time, it is necessary to solve the problem of coherence of the proposal (offensive plan) and obtain the approval of the majority of the generals to solve the problem of the Byzantine generals.

The situation is similar in blockchain networks.

In a distributed blockchain network, there may be multiple people requesting a batch of blocks, and there may be fake blocks among them, so the distributed consensus algorithm can only solve this problem.

We know that one of the core values of blockchain is consensus, which is also one of the characteristics of blockchain that everyone strives for. Today we will focus on how blockchain solves the above problems with the help of a “consensus mechanism”.

In fact, the concept of a consensus mechanism did not arise from the development of blockchain. This direction in mathematics, especially in the field of computing, has long been a scientific and conquered direction. There are already several well known solutions. for distributed consensus mechanisms., has achieved very remarkable achievements.

Blockchain is a scenario where the “consensus mechanism” is fully applied.

What is a consensus algorithm?

Consensus Algorithm As the name suggests, it is a scheme that allows all participants to agree on a certain outcome through algorithmic means. In blockchain, it refers to finding a trusted strategy for transmitting and verifying information among untrusted parties in an untrusted network environment.

However, reliability here is also conditional: illegal nodes must be controlled in a certain proportion to guarantee reliability. There are many types of consensus algorithms. Bitcoin currently uses a proof-of-work consensus mechanism.

Why does blockchain need a consensus algorithm?

Let's take Bitcoin for example. In the Bitcoin blockchain network, since it is decentralized, all nodes are equal and each node will have a ledger that can maintain accounts, and then there will be many different ledgers.

But in reality, we need everyone to own the same ledger to ensure system data is consistent and the system can operate efficiently.

So, how to ensure that only one node is allowed to create legal ledgers for a certain period of time, to ensure that all ledgers are consistent (at least most people's ledgers are consistent), how to audit legal ledgers and identify illegal ledgers?

These issues must be resolved in a decentralized blockchain network, otherwise anyone can tamper with the contents of the ledger at will and then claim that their own ledger is legitimate. In this case, the Bitcoin system will be broken.

How does Bitcoin solve this problem? It uses the PoW (Proof of Work) consensus algorithm. This algorithm can not only ensure that the number of proposals (requests for accounting) that appear on the network within a certain period of time is limited, but also abandon the requirement of strict consistency and move towards the requirement of eventual consistency (that is, allowing at the same time). time in the chain There are several legal blocks, and the link branches, but in the end, the link with the heaviest workload, i.e. the longest chain, will be the last legal chain)

What consensus algorithms, besides Bitcoin, are used in other token blockchain networks?

What are the consensus algorithms?

There are many consensus algorithms, including PBFT (Practical Byzantine Fault Tolerance), PoW (Proof of Work), PoS (Proof of Stake) and DPoS (Delegate Proof of Stake), Ripple and distributed consensus algorithms (Pasox, Raft), etc. etc. Each algorithm has its own gameplay.

Here are some of the most commonly used blockchains:

PoW (Proof of Work)

Both Bitcoin and Ethereum are implemented based on this algorithm. Simply put, PoW is proof that a certain amount of work has been done on the production side. The main feature of the PoW system is the asymmetry of computation. The end of the work must perform a certain degree of complexity to obtain the result, but the verifier can easily check whether the end of the work has performed the corresponding work through the result, haha, this As they say, the work is difficult to perform, and inspection is easily.

In the Bitcoin system, a round of competition for computing power begins approximately every 10 minutes. Each performs SHA256 operations on a specific string + random nonce and expects to receive a value that matches the system's expectations. If the calculated result does not match the expected value, the nonce value is continually adjusted and recalculated until the expected value is reached. So it's hard to find the expected value and there is no shortcut. You have to constantly try the nonce value, which requires huge calculations. This is the so-called mining (here, for ease of understanding, the working principle is roughly presented, and I will present it in another article about the blockchain hash algorithm).

If a particular node is lucky and the calculated result just matches the expected value, then that node must inform other nodes throughout the network so that other nodes can verify that it is working correctly. It is very easy for others to check the amount of calculation, so PoW is an algorithm for calculating power asymmetry. If the other nodes have been quickly verified and there are no problems, then that lucky node has the right to maintain the accounts and can put the newly packaged block into the blockchain.

PoW characteristics:

Fully decentralized, nodes can move in and out freely
As long as the computing power of illegal nodes in the network does not exceed 50%, this verification method is reliable.
Causes a lot of wastage of computing resources (because this random number mining behavior consumes the GPU and other computing power, but does not create value)

Therefore, the advantages and disadvantages of PoW are quite obvious, especially the problem of computing power consumption is often criticized in Bitcoin. Therefore, the goal of Ethereum planning is to switch to the PoS algorithm.

PoS (Proof of Stake, proof of fairness)

The PoS algorithm solves the PoW energy consumption problem. POS is called proof of fairness or proof of fairness. It is actually a consensus mechanism that requires each node to provide proof of a certain amount of virtual currency in order to compete for blockchain accounting rights.

According to the PoS model, the accounting right no longer has a higher probability of accounting for the one who has more hashing power like PoW, but the one with more tokens is more likely to get the accounting rights. As you can imagine, PoW is like more work and PoS is like rich people.

Relying solely on the number of tokens to allocate accounting rights will likely lead to centralization of accounting rights. Therefore, in the competition for accounting rights, some token systems will not only count who has more tokens, but also count holdings. Time length of a token, for example Pidiancoin.

Although PoS clearly solves the problem of computing power and reduces the time to reach consensus. However, the PoS algorithm may also introduce some new problems. For example, due to the Matthew effect, the decision-making power and benefits of the system will be increasingly concentrated in the hands of a few people, losing fairness. Additionally, PoS systems are vulnerable to “fork attacks,” leading to problems such as “double payment.”

Hence, the POS algorithm has also undergone various changes and updates such as the DPos algorithm.

DPoS (Delegate Proof of Stake)

The DPos algorithm is called proof of trust or proof of trust capital. Compared to PoW and PoS, it further improves the efficiency of the blockchain.

The DPoS mechanism does not require all nodes in the network to participate in creating and validating a block. From time to time, it selects a small group of nodes and allows this small group of nodes to create and verify the blockchain. Network resource consumption is further reduced, and the operating efficiency of a blockchain such as EOS is also increased.

But how is this small group of nodes determined? In fact, everyone votes for him. In a DPoS system, each token is a vote that takes full advantage of shareholder voting to reach consensus in a fair manner. Everyone selects N witnesses (that is, N witnesses). Mining pool) these N witnesses have equal power, and only witnesses can create and manage blocks. In addition, shareholders may vote to replace these witnesses at any time.

There are some other consensus algorithms that are not covered here. In blockchain, due to the different scenarios of each project, the developed architecture and the adopted consensus algorithm are not the same. Mainly from three elements: decentralization, security and performance, different combinations are created according to different application scenarios.

Recommended reading

Using Redis5 basic types in java

LinkedHashMap basic analysis

Interpretation of the Mybatis plugin at the source code level