Introduction to SHA256
SHA256 is an algorithm subdivided under SHA-2.
SHA-2, the name comes from the acronym Secure Hash Algorithm 2, a cryptographic hash function algorithm standard developed by the National Security Agency, is one of the SHA algorithms, it is SHA-1 Successor.
According to SHA-2, it can be divided into six different algorithm standards.
Including: SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, SHA-512/256.
Apart from some minor differences in summary length and number of loops, the basic structure of the algorithm is consistent.
Returning to SHA256, frankly speaking, it is a hash function.
Hash functions, also known as hashing algorithms, are a method of creating small digital fingerprints from any data. A hash function compresses the message or data into a digest, reducing the amount of data and fixing the format of the data. This function shuffles the data and recreates a fingerprint called a hash value (or hash value). The hash value is usually represented by a short string of random letters and numbers.
For messages of any length, SHA256 generates a 256-bit hash value called the message digest.
This summary is equivalent to a 32 byte long array, typically represented by a hexadecimal string of length 64
Let's look at an example:
Become a blockchain programmer for 100 days and the uncle of the Red Army leads us by fighting!
In this sentence, the hash value obtained after the SHA256 hash function is:
A7FCFC6B5269BDCCE571798D618EA219A68B96CB87A0E21080C2E758D23E4CE9
Found one here SHA256 online verification tool. Can be used to check the SHA256 hashing result and also to check if the SHA256 code is correct. It is very convenient to use, you can feel it.
What is a hash function?
The three main purposes of hash functions are:
- Encrypt data deterministically (this type of encryption always produces the same encrypted value for the same text value);
- Accept input of any length and output a fixed length result;
- Changing data is irreversible. Input cannot be obtained from output.
SHA-2 fulfills them fully. If you want to learn more about hash functions, there are several suitable publications on Habré. For example, the articles “What is hashing? Under the hood of the blockchain" and "Hash algorithms".
Detailed explanation of the SHA256 principle
To better understand the principle of SHA256, here are the modules that can be extracted separately from the algorithm, including Persistent initialization、Information pre-processing、Boolean operations used Introducing separately, after getting rid of these barriers in understanding, let's look at the main part of the SHA256 algorithm, i.e. How the message digest is calculated.
2.1 Persistent initialization
8 initial hash values and 64 hash constants are used in the SHA256 algorithm
Among them, the SHA256 algorithm 8 initial hash values are as follows:
h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19
These seeds are obtained by taking the first 32 bits of the fractional part of the square root of the first 8 prime numbers (2, 3, 5, 7, 11, 11, 13, 17 and 19) into natural numbers
For example, 2–√ 2 The fractional part is about 0.414213562373095048, and
0.414213562373095048≈6∗16−1+a∗16−2+0∗16−3+… 0.414213562373095048 ≈ 6 ∗ 16 − 1 + a ∗ 16 − 2 + 0 ∗ 16 − 3 + . . . Therefore, the fractional part of the square root of the prime number 2 is the first 32 bits and corresponds to 0x6a09e667
The SHA256 algorithm uses 64 constants as follows:
428a2f98 71374491 b5c0fbcf e9b5dba5 3956c25b 59f111f1 923f82a4 ab1c5ed5 d807aa98 12835b01 243185be 550c7dc3 72be5d74 80deb1fe 9bdc06a7 c 19bf174 e49b69c1 efbe4786 0fc19dc6 240ca1cc 2de92c6f 4a7484aa 5cb0a9dc 76f988da 983e5152 a831c66d b00327c8 bf597fc7 c6e00bf3 d5a79147 06ca 6351 14292967 27b70a85 2e1b2138 4d2c6dfc 53380d13 650a7354 766a0abb 81c2c92e 92722c85 a2bfe8a1 a81a664b c24b8b70 c76c51a3 d192e819 d6 990624 f40e3585 106aa070 19a4c116 1e376c08 2748774c 34b0bcb5 391c0cb3 4ed8aa4a 5b9cca4f 682e6ff3 748f82ee 78a5636f 84c87814 8cc70208 90befffa a4506ceb bef9a3f7 c67178f2
Like the 8 hash seeds, these constants are the first 64 prime numbers in the natural number (2,3,5,7,11,13,17,19,23,29,31,37,41,43,47, 53,59 ,61,67,71,73,79,83,89,97...) the fractional part of the cube root comes from the first 32 bits.
2.2 Pre-processing of information (pre-processing)
Pre-processing in the SHA256 algorithm involves adding the necessary information after the message you want to hash so that the entire message follows a given structure.
Information preprocessing is divided into two stages: Additional padding bits with Additional length
STEP1: Additional padding bits
Pad the end of the message so that the remaining message length after modulus 512 is 448
The padding is done so that the first bit is filled with 1s and then both are filled with 0s until the length is modulo 512 and the remainder is 448.
It should be noted that the information must be padded, that is, even if the length satisfied the remainder after modulo 512 was 448, the padding bits must also be performed to fill the 512 bits.
Therefore, padding must pad at least one bit and up to 512 bits.
example : Use the message "abc" as an example to show the filling process.
corresponds to a, b, c ASCII code 97, 98, 99 respectively
So, the binary code of the original information: 01100001 01100010 01100011
First step to fill the position, first fill in "1": 0110000101100010 01100011 1
At the second stage of filling, 423 “0” are filled: 01100001 01100010 01100011 10000000 00000000… 00000000
The data after bit completion is completed looks like this (in hexadecimal for reference):
61626380 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
Why 448?
Because after the first stage of preprocessing, the second stage will add 64-bit data indicating the length of the original message. And 448 + 64 = 512, which is simply the complete structure.
STEP2: additional length value
The additional length value is to add information about the length of the original data (the message before the first padding step) to the message after the padding operation is completed.
Original text given on Wikipedia: append length of message (before pre-processing), in bits, as 64-bit big-endian integer
SHA256 uses 64-bit data to represent the length of the original message.
Therefore, the message length calculated by SHA256 must be less than 264 2 6 4 Of course, in most cases this is quite large.
The method for encoding length information is a 64-bit little-endian integer
onBig endianThe meaning is given at the end of the article
Now back to the example, the message "abc", 3 characters, occupies 24 bits.
So after the length padding operation the whole message becomes as follows (hexadecimal format)
61626380 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000018
2.3 Logical operations
All operations performed in the SHA256 hash function are logical bit operations.
Including the following logic functions:
Ch(x,y,z)=(x∧y)⊕(¬x∧z) C h ( x , y , z ) = ( x ∧ y ) ⊕ ( ¬ x ∧ z )
Ma(x,y,z)=(x∧y)⊕(x∧z)⊕(y∧z) M a ( x , y , z ) = ( x ∧ y ) ⊕ ( x ∧ z ) ⊕ ( y ∧z)
Σ0(x)=S2(x)⊕S13(x)⊕S22(x) Σ 0 ( x ) = S 2 ( x ) ⊕ S 13 ( x ) ⊕ S 22 ( x )
Σ1(x)=S6(x)⊕S11(x)⊕S25(x) Σ 1 ( x ) = S 6 ( x ) ⊕ S 11 ( x ) ⊕ S 25 ( x )
σ0(x)=S7(x)⊕S18(x)⊕R3(x) σ 0 ( x ) = S 7 ( x ) ⊕ S 18 ( x ) ⊕ R 3 ( x )
σ1(x)=S17(x)⊕S19(x)⊕R10(x) σ 1 ( x ) = S 17 ( x ) ⊕ S 19 ( x ) ⊕ R 10 ( x )
Where:
| logical operation | meaning |
| ∧ ∧ | Bitwise AND |
| ¬ ¬ | Bitwise "complement" |
| ⊕ ⊕ | Bitwise XOR |
| Sn S n | Right shift n bits |
| Rn Rn | Rotate right n bits |
2.4 Calculate message digest
Now let's get acquainted with the main part of the SHA256 algorithm, that is, how the message digest is calculated.
First: break the message into 512-bit blocks
(break message into 512-bit chunks)
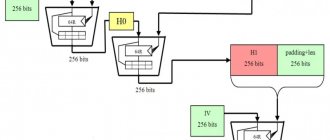
Assume that message M can be decomposed into n blocks, so all the algorithm needs to do is perform n iterations, and the result of n iterations is the final hash value, which is a 256-bit digital digest.
The initial value of the 256-bit digest, H0, is computed through the first block of data to obtain H1, which is the first iteration.
H1 receives H2 through the second block of data, ..., processes it in turn and finally receives Hn, which is the final digest of the 256-bit message
Use the mapping for each iteration Map(Hi−1)=Hi M ap ( H i − 1 ) = H i Means the iteration can be displayed more vividly as:
256 bits in the picture Hi There are 8 small blocks described, this is because the smallest arithmetic unit in the SHA256 algorithm is called “Word” (Word), a word is 32 bits.
Additionally, in the first iteration, the initial value of the map is set to 8 initial values of the hash entered earlier, as shown in the following figure:
The following begins to introduce the content of each iteration, that is, the mapping Map(Hi−1)=Hi M ap ( H i − 1 ) = H i Specific algorithm
STEP 1: Construct 64 words
break chunk into sixteen 32-bit big-endian words w[0], …, w[15]
For each block, decompose the block into 16 32-bit little-endian words, denoted w[0],..., w[15]
In other words, the first 16 words are directly decomposed from the i-th message block.
The remaining words are obtained using the following iterative formula:
Wt=σ1(Wt−2)+Wt−7+σ0(Wt−15)+Wt−16 W t = σ 1 ( W t − 2 ) + W t − 7 + σ 0 ( W t − 15 ) + W t − 16
STEP 2: 64 cycles
map Map(Hi−1)=Hi M ap ( H i − 1 ) = H i Contains 64 encryption cycles
That is, 64 encryption cycles can be performed to complete one iteration
Each encryption cycle can be described by the following figure:
In the figure, 8 words ABCDEFGH are updated according to certain rules, among which
The blue squares are the predefined nonlinear logic functions that were laid out above.
The red box square represents the mod 232 2 32 Also, two numbers are added together, if the result is greater than 232 2 32, you must divide by 232 2 32 and find the remainder.
Initial values ABCDEFGH at the beginning Hi−1(0),Hi−1(1),…,Hi−1(7) H i − 1 ( 0 ) , Hi − 1 ( 1 ) , . . . , H i − 1 ( 7 )
Kt is the t-th key corresponding to the 64 constants that we mentioned above
Wt is the t-th word generated in this block. The original message is broken into 512-bit fixed-length blocks, and 64 words are generated for each block. The eight words ABCDEFGH are round-robin encrypted by repeating the loop n times.
The eight characters generated by the last loop are the hash string corresponding to the i-th block. Hi H i
This change completes all introductions to the SHA256 algorithm
Application:
Python Sha256 is used in some of the most popular encryption and authentication protocols, such as:
- href=»https://en.wikipedia.org/wiki/Secure_Sockets_Layer»>SSL: href=»https://en.wikipedia.org/wiki/Secure_Sockets_Layer»>SSL: secure sockets layer
- TLS: Transport Layer Security
- IPSec: Internet Protocol Security
- SSH: secure shell
Sha256 is also used in unix and linux to protect passwords using a hash.
SHA256 pseudocode algorithm
Now we can combine the pseudocode of the SHA256 algorithm and comb through all the above steps:
Note: All variables are unsigned 32 bits and wrap modulo 232 when calculating Initialize variables (first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19): h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19 Initialize table of round constants (first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..31 1): k [0..63]: = 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59F111F1, 0x923F82A4, 0xab1c5ed5, 0xd807AA98, 0x12835B01, 0x 5BE, 0x550C7DC3, 0x72BE5D74, 0x80DEB1FE, 0x9BDC06A7, 0XC19BF174, 0XE49B69C1, 0XEFBE4786, 0X0FC19DC6, 0x240CA1CC, 0x2DE92C6C,, 0x240CA1CC. 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x142 92967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f8 2ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 Pre-processing: append the bit '1' to the message append k bits '0', where k is the minimum number >= 0 such that the resulting message length (in bits) is congruent to 448(mod 512) append length of message (before pre-processing), in bits, as 64-bit big-endian integer Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk break chunk into sixteen 32-bit big-endian words w[0..15] Extend the sixteen 32-bit words into sixty-four 32-bit words: for i from 16 to 63 s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor(w[i-15] rightshift 3) s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor(w[i-2] rightshift 10) w :
= w[i-16] + s0 + w[i- 7] + s1 Initialize hash value for this chunk: a := h0 b := h1 c := h2 d := h3 e := h4 f := h5 g := h6 h := h7 Main loop: for i from 0 to 63 s0 := (a rightrotate 2) xor (a rightrotate 13) xor(a rightrotate 22) maj := (a and b) xor (a and c) xor(b and c) t2 := s0 + maj s1 : = (e rightrotate 6) xor (e rightrotate 11) xor(e rightrotate 25) ch := (e and f) xor ((not e) and g) t1 := h + s1 + ch + k + w h : = gg := ff := ee := d + t1 d := cc := bb := aa := t1 + t2 Add this chunk's hash to result so far: h0 := h0 + a h1 := h1 + b h2 : = h2 + c h3 := h3 + d h4 := h4 + e h5 := h5 + f h6 := h6 + g h7 := h7 + h Produce the final hash value (big-endian): digest = hash = h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
Preface
The most commonly used encryption algorithm among all encryption algorithms is hash encryption. The encryption algorithms that many people encounter for the first time, such as MD5 and SHA1, are typical hash encryption algorithms, and hash encryption is not only used to encrypt passwords, but there are many applications such as extracting content summaries, generating signatures, comparing documents , block chain and so on. This article details hash encryption and introduces the hash encryption tool class.
JAVA Tools
package cn.hengyumo.humor.utils;
import org.apache.commons.codec.binary.Base64; import org.apache.commons.codec.binary.Hex; import javax.crypto.Mac; import javax.crypto.spec.SecretKeySpec; import java.security.MessageDigest; import java.security.NoSuchAlgorithmException; /** * HeaUtil * Hash encryption algorithm * Hash encryption algorithm: MD5, SHA-1, SHA-256, HMAC-SHA-1, HMAC-SHA-256 * Package org.apache.commons.codec must be imported * * @author hengyumo * @version 1.0 * @since 2019/11/12 */ @SuppressWarnings("WeakerAccess") public class HeaUtil { /** * md5 encryption * * @param text content * @return digest summary * @throws NoSuchAlgorithmException e */ public static String md5(String text) throws NoSuchAlgorithmException { MessageDigest messageDigest = MessageDigest.getInstance("MD5"); byte[] bytes = messageDigest.digest(text.getBytes()); return Hex.encodeHexString(bytes); } /** * sha1 encryption * * @param text content * @return digest summary * @throws NoSuchAlgorithmException e */ public static String sha1(String text) throws NoSuchAlgorithmException { MessageDigest messageDigest = MessageDigest.getInstance("SHA-1"); byte[] bytes = messageDigest.digest(text.getBytes()); return Hex.encodeHexString(bytes); } /** * sha256 encryption * * @param text content * @return digest summary * @throws NoSuchAlgorithmException e */ public static String sha256(String text) throws NoSuchAlgorithmException { MessageDigest messageDigest = MessageDigest.getInstance("SHA-256"); byte[] bytes = messageDigest.digest(text.getBytes()); return Hex.encodeHexString(bytes); } /** * encrypt hmac-sha1 * * @param text content * key @param key * * @ return ciphertext * @throws Exception e */ public static String hmacSha1(String text, String key) throws Exception { SecretKeySpec sk = new SecretKeySpec(key.getBytes(), "HmacSHA1"); return hmacSha1(text, sk); } /** * encrypt hmac-sha1 * * @param text content * @param sk key * * @ return ciphertext * @throws Exception e */ public static String hmacSha1(String text, SecretKeySpec sk) throws Exception { Mac mac = Mac.getInstance("HmacSHA1"); mac.init(sk); byte[] rawHmac = mac.doFinal(text.getBytes()); return new String(Base64.encodeBase64(rawHmac)); } /** * Create key HmacSha1 * * @param key key string * @return SecretKeySpec */ public static SecretKeySpec createHmacSha1Key(String key) { return new SecretKeySpec(key.getBytes(), "HmacSHA1"); } /** * hmac-sha256 encryption * * @param text content * key @param key * * @ return ciphertext * @throws Exception e */ public static String hmacSha256(String text, String key) throws Exception { SecretKeySpec sk = new SecretKeySpec(key.getBytes(), "HmacSHA256"); return hmacSha1(text, sk); } /** * hmac-sha256 encryption * * @param text content * @param sk key * * @ return ciphertext * @throws Exception e */ public static String hmacSha256(String text, SecretKeySpec sk) throws Exception { Mac mac = Mac.getInstance("HmacSHA256"); mac.init(sk); byte[] rawHmac = mac.doFinal(text.getBytes()); return new String(Base64.encodeBase64(rawHmac)); } /** * Generate key HmacSha256 * * @param key key string * @return SecretKeySpec */ public static SecretKeySpec createHmacSha256Key(String key) { return new SecretKeySpec(key.getBytes(), "HmacSHA256"); } /** * Test task * * @param args args */ public static void main(String[] args) throws Exception { String s = "123456789 dislike, dislike"; System.out.println(md5(s)); System.out.println(sha1(s)); System.out.println(sha256(s)); String k = ""; System.out.println(hmacSha1(s, k)); s = "aeqnfoavneornqoenr1, but I can't understand the situation in the south 010jownfasdfqijqor"; System.out.println(hmacSha1(s, k)); SecretKeySpec sk1 = createHmacSha1Key(k); System.out.println(hmacSha1(s, sk1)); SecretKeySpec sk256 = createHmacSha256Key(k); System.out.println(hmacSha256(s, sk256)); } } Conclusion
d415ffe55bf2e18b9e059be4ab371fe7 15b03a4189d24ca3459e199bbf8de7fc3e4d68f3 e32b84b738416e91198112a57d295ba685a40e55bb114725e8a444efd53d5 a01 ck66ZAkPEh+19UIgnX775N3nLyc= WVJAs/+6OlwkzM1ZEK+t8iMgtyc= WVJAs/+6OlwkzM1ZEK+t8iMgtyc= E1sXoiPtnjzMiDRagp08Lt3gBKXE/EU+nLJZpy8hURc=
Notes
Use the need to import maven package or jar
commons-codec commons-codec 1.12