Over the years, statisticians, economists and mathematicians have developed several methods to measure the performance of tradable assets such as stocks, commodities and currencies.
One such measure is the Sharpe ratio , which was introduced in 1966 by William Sharpe: professor emeritus of finance at Stanford.
Since then, this ratio has proven to be a valuable tool used by investors to evaluate the return on an investment compared to its risk.
The Sharpe ratio is popular among traders and fund/portfolio managers due to its simplicity. Another reason for its popularity is the fact that Professor Sharp received the 1990 Nobel Prize in Economic Sciences. For this reason, investors regularly use it when buying stocks.
What is Sharpe Ratio?
The Sharpe ratio is a metric used by investors to better understand the return on an investment per unit of risk.
This ratio allows investors to determine how much of the profit they will receive depending on the volatility they will experience while holding the asset.
This means that an asset or portfolio with a higher Sharpe ratio is considered a better choice compared to other investments in the same category.
This higher ratio simply results in high returns with minimal investment risk.
Benchmark for the entire industry
The Sharpe ratio is one of the most popular benchmarks for the asset management industry. It compares different funds and portfolios, evaluates the manager’s performance and the historical results of strategies. After all, the relationship between return and risk is the most important thing in investing, and the Sharpe ratio shows what kind of return an investor receives per unit of risk. The higher the value, the better the risk-adjusted return. The metric has become so popular and widely accepted that every investment resource (Bloomberg, Google Finance, Morningstar, etc.) uses it to rank every ETF, mutual fund, hedge fund trading strategy, and entire asset class. Perhaps, where it cannot be found is on the pages with descriptions of OPIF.
Sharpe Ratio
shows how much return an investor receives per unit of risk. The higher the value, the better the risk-adjusted return. The coefficient was created for the analysis of portfolios, not individual instruments.
Sharpe ratio calculation
When calculating the Sharpe ratio, the following formula is used:
Sharpe ratio = (R x - R f) / StdDev (R x)
Definition of terms:
- x = investment being analyzed
- R x = expected return on investment
- R f = risk-free rate of return
- StdDev(Rx) = standard deviation R x
We can further refine the terms as follows: The investment can be a security, a portfolio, a currency, or a new asset class. The expected return on an investment is what the investor expects to receive within a specified time frame.
This can be determined using different time periods: daily, weekly, monthly or yearly.
The risk-free rate of return is the theoretical rate of return on an investment with zero risk. In most cases, users of the Sharpe ratio like to use the yield on the shortest dated government T-Bill.
By making such calculations, investors consider T-Bill to be the safest asset in the financial markets since it is backed by the Ministry of Finance.
The last term in the Sharpe ratio equation is the standard deviation of the asset being analyzed. As with all standard deviations, it is a measure of the amount of change in the value of an asset over a specified period of time. Standard deviation gives a clear picture of the historical volatility of the asset being analyzed.
When a metric becomes a goal, it is no longer a good metric.
The more a quantitative indicator is used for decision making, the more it is subject to various “improvements.” The problem is that using a simple Sharpe ratio formula over the same time period for the same fund can produce completely different data. Consider data from the largest providers of information on asset-weighted hedge fund performance: the HFRI Fund of Funds Composite Index and the Credit Suisse Broad Hedge Fund Index. They publish Sharpe ratios of 0.81 and 0.8 for the period from 1990 to 2022 and use the monthly performance of the index to estimate its volatility. Unfortunately, calculating volatility using monthly data underestimates annualized volatility by about 40%, resulting in an inflated Sharpe ratio. It turns out that by using different data frequencies when calculating volatility, you can manipulate the value of this indicator and this will not be considered cheating.
Sharpe is indeed a good and generally accepted metric for assessing a portfolio's historical return-to-risk ratio. However, it makes no sense to rely solely on it when making investment decisions and building a portfolio.
[1] https://www.institutionalinvestor.com/article/b1p62z599ns4pd/The-Sharpe-Ratio-Broke-Investors-Brains
[2] https://www.sec.gov/Archives/edgar/data/1479026/000119312516453980/d55076d485apos.htm
Comparison of Sharpe's Ex-Ante and Ex-Post
One of the benefits of the Sharpe ratio is flexibility in choosing the type of performance data to enter into your calculations.
On the one hand, the Sharpe ratio can be used to evaluate the past performance of an investment or portfolio. In this case, actual earnings are used in the formula.
This Sharpe ratio is called "Ex-Post". The term "Ex-Post" means "after the fact." Such a Sharpe ratio can be further used to predict future returns from investment choices with sufficient past data.
In the case of an investment or portfolio without adequate historical performance data, an investor may use expected performance to calculate what is known as the Sharpe Ex-Ante Ratio.
The term "Ex-Ante" means "before the fact" and this Sharpe ratio is based on estimates and/or forecast performance.
What does the Sharpe ratio tell us?
Through the general formula and its individual components, we also understand that the Sharpe ratio gives us a quantitative assessment of the effectiveness of an investment choice in relation to the risk taken when owning an asset.
Once the Sharpe ratio has been determined, potential investments can be classified as follows:
A value less than 1 means a bad investment.
- A sharper ratio of 1 - 1.99 means an adequate or good investment
- 2 – 2.99 – very good investment
- More than 3 is considered an excellent investment choice
For example, suppose we are analyzing two different portfolios that contain different stocks. After the necessary calculations, the first portfolio is determined to provide a return of 14%.
However, with such high returns, there is usually high volatility. In this case, volatility was determined to be 9%.
The second portfolio has also been evaluated and has the potential to provide a return of 8.5% with lower volatility of 4%. Using a hypothetical Treasury Bill with a risk-free return of 3%, we obtain the following comparisons between the two portfolios.
| 1st portfolio | 2nd portfolio | |
| Profit rate | 14 | 8.5 |
| Risk-free rate of return | 3 | 3 |
| Volatility | 9 | 4 |
| Sharpe ratio | (14-3) / 9 = 1,22 | (8,5-3) / 4 = 1,375 |
All investments are aimed at maximizing profit and at the same time reducing risk. In this case, a second portfolio is desirable.
Additionally, by using these two examples, we further understand the exponential relationship between asset volatility and Sharpe ratio.
The lower the volatility, the higher the Sharpe ratio. Conversely, the higher the volatility, the lower the Sharpe ratio.
Caveats regarding the use of the Sharpe ratio.
The Sharpe ratio is the basis for assessing the performance of financial assets. But there are two caveats to its use: one has to do with the interpretation of negative Sharpe ratios and the other has to do with conceptual limitations.
Financial theory tells us that over the long term, investors should be compensated for the additional average return above the risk-free rate to accept additional risk, at least if the risky portfolio is well diversified. If investors receive such compensation, the numerator of the Sharpe ratio will be positive.
However, we often find that portfolios exhibit negative Sharpe ratios when the ratio is calculated over periods dominated by bear equity markets. This increases caution when working with negative Sharpe ratios.
When working with positive Sharpe ratios, the Sharpe ratio for a portfolio decreases as we increase risk, all other things being equal.
This result is intuitive for assessing risk-adjusted effectiveness. However, with negative Sharpe ratios, an increase in risk results in an increase in the Sharpe ratio in numerical terms (for example, doubling the risk could increase the Sharpe ratio from -1 to -0.5).
Therefore, when comparing portfolios with negative Sharpe ratios, we generally cannot assume that a larger Sharpe ratio (one closer to zero) means better risk-adjusted performance.
However, if the standard deviations are equal, a portfolio with a negative Sharpe ratio close to zero has an advantage.
In practice, to make an interpretable comparison using the Sharpe ratio, we may need to extend the estimation period so that one or more Sharpe ratios become positive. The financial analyst may also consider using another metric to measure performance.
A conceptual limitation of the Sharpe ratio is that it only considers one aspect of risk—the standard deviation of returns. Standard deviation is the most appropriate measure of risk for portfolio strategies with approximately symmetric return distributions. Strategies with options elements have asymmetric returns.
Accordingly, an investment strategy may produce frequent small gains but has the potential to result in infrequent but extremely large losses. This statement describes an inverse distribution with negative skewness. We'll discuss asymmetry later.
This strategy is sometimes figuratively described as “collecting coins in front of a bulldozer.” For example, some hedge fund strategies tend to have a similar return pattern.
Calculated over the period during which the strategy operates (i.e. no major losses occurred), this type of strategy will have a high Sharpe ratio. In this case, the Sharpe ratio would give an overly optimistic picture of risk-adjusted performance because the standard deviation does not fully measure the risk taken by investors.
Therefore, before applying the Sharpe ratio to evaluate a manager's performance, we must evaluate whether the standard deviation adequately describes the risk of the manager's investment strategy.
The example below illustrates the calculation of the Sharpe ratio in the context of assessing portfolio performance.
Disadvantages of the Sharpe ratio
One of the disadvantages of the Sharpe ratio is its use of the standard deviation of returns to measure investment returns.
Standard deviation is based on the assumption that income is distributed evenly. However, traders and investors know that price movements in financial markets are not always distributed evenly over a period of time.
Some trading days see a significant spike due to some random event. On other days, the market is in the red due to traders capitalizing on the apparent opportunity to go short based on technical indicators.
The second disadvantage of the Sharpe ratio is the simple ability of some portfolio managers to manipulate their resources to enhance their reputation. This can be done by using a longer time period to measure volatility, which results in a lower value.
A portfolio manager may decide to use the standard deviation over a period of several months rather than a few days. The first data set provides a lower estimate of volatility compared to the second.
Third, the portfolio manager may decide to sample data over a period of time when volatility was uniform or absent. Thus, by deliberately selecting a data set, a portfolio manager can distort the final value of the Sharpe ratio for its own benefit.
The difference between Sharpe and Sortino
It is because of some of these limitations of the Sharpe ratio that some fund managers and traders prefer to use the Sortino ratio.
Unlike the Sharpe ratio, the Sortino ratio does not take into account the overall volatility of an investment. It measures the performance of an investment relative to the downside risk of the investment.
Sortino coefficient = (R x - R f ) / StdDev d
Definition of terms:
- x = investment
- >R x = expected return on investment
- R f = risk-free rate of return
- StdDev d = standard deviation of negative return on assets
There is no point in looking at the Sharpe ratio of individual instruments
By composing a portfolio of two different instruments with a certain Sharpe ratio, the resulting portfolio will not be
have a weighted average of the Sharpe ratio of the two assets. It's all about correlation. For example, let's take two funds with the following characteristics (see table 1).
Table 1. Comparison of the Sharpe ratio of two individual assets and a portfolio of them
| Return above the risk-free rate | Volatility | Sharpe ratio | |
| Asset A | 12% | 10% | 1,2 |
| Asset B | 10% | 10% | 1,0 |
| Total portfolio (asset correlation - 0.5) | 11% | 8,7% | 1,27 |
As you can see, the Sharpe for the final portfolio is higher than for the two assets separately.
Conclusion
To summarize, retail and institutional investors need a proper method for quantifying return versus risk when making investment choices.
Forecasting potential returns is not sufficient when assessing the viability of an investment over a period of time.
The Sharpe ratio provides a better understanding of the attractiveness of an investment by incorporating risk into its calculation. This allows investors to better understand the return relative to the risk taken in owning the asset.
However, as with all things, the Sharpe ratio has its drawbacks. It uses standard deviation assuming that returns are distributed evenly. Because of this, some traders and investors prefer to use the Sortino ratio, which uses only the downward standard deviation in its calculation.
Sharpe may vary
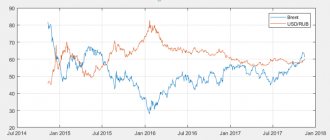
Jack Bogle once said, “In terms of how the Sharpe ratio ranks mutual funds, I would say bad.” And it’s hard to disagree with this. Today, every management company actively promotes the Sharpe ratios of its funds in marketing materials. But Sharpe, like its components, can change over time. For example, the Sharpe ratio of the S&P index from 2009 to 2022 managed to be both negative and rise to level 6 (see Figure 1).
Source: PortfolioVisualizer.com